アフィン空間（読み）アフィンくうかん（英語表記）affine space

ブリタニカ国際大百科事典 小項目事典

アフィン空間
アフィンくうかん
affine space

疑似空間ともいう。その空間の上の移動が，ベクトルとして考えられる空間のことである。数学的に厳密に定式化するには，次のようにする。点集合 A と n 次元ベクトル V を考え，A の任意の2点 P₁ ，P₂ (順序も考える) に対して，V の 1 つのベクトル を次のように対応させるとき，集合 A は n 次元アフィン空間と呼ばれる。
(1) 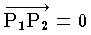( 0 は零ベクトル) が成立するための必要十分条件は，P₁ ，P₂ が一致することである。
(2) 集合 A の任意の3点 P₁ ，P₂ ，P₃ に対して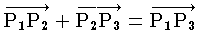， が成り立つ。
(3) 集合 A の任意の点 P₁ と V の任意のベクトル a について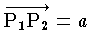， が成り立つような A の点 P₂ が存在し，これが一意的に定まる。
V は A に付随する基本ベクトル空間と呼ばれる。特に, 付随する基本ベクトル空間がユークリッドベクトル空間であるようなアフィン空間をユークリッド空間という。ユークリッド空間の2点 P₁ ，P₂ の距離は，ベクトル の長さ ｜a｜ であると定義する。アフィン空間 A の部分集合 B ( B は空集合でないとする) が，部分アフィン空間であるとは，B の点 P に対応して定まるベクトル 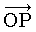( O は B の定点) の全体が，ベクトル空間となる場合である。たとえば, 3次元アフィン空間の，1次元および2次元部分アフィン空間は，普通の空間の直線および平面である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

アフィン空間【アフィンくうかん】

擬似(ぎじ)空間とも。ユークリッド空間から長さと角の大きさの概念を捨象して得られる空間。点集合Aとベクトル空間Vがあり，Aの任意の点pとVの任意のベクトルxに対し和p＋xが定義されていて，1.Vの任意のベクトルv，uに関し（p＋v）＋u＝p＋（v＋u），2.Aの任意の点p，qに対しq＝p＋vとなるVのベクトルvがただ一つ存在する，という２公理がみたされるとき，Aをアフィン空間といい，Vをアフィン空間Aに付属するベクトル空間という。→アフィン幾何学
→関連項目空間（数学）

出典　株式会社平凡社

世界大百科事典内のアフィン空間の言及

【アフィン幾何学】より

…したがってアフィン幾何学では，平面や空間のもっている長さなどの計量構造は意味をもたなくなるが，直線，交点などのような線形構造はそのまま残る。平面や空間からその計量構造を捨てて線形構造のみを考えた場合，これらをアフィン平面，アフィン空間という。　アフィン幾何学でも三角形という概念は意味をもつが，ユークリッド幾何学では無数の異なる三角形が存在するのに対し，アフィン幾何学では〈すべての三角形は相等しい〉という定理が成り立つ。…

※「アフィン空間」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社