カバリエリの原理（読み）カバリエリノゲンリ（その他表記）principle of Cavalieri

デジタル大辞泉

カバリエリ‐の‐げんり【カバリエリの原理】

二つの立体を一定の平面に平行な平面で切ったとき、切り口の面積の比が等しければ、この二つの立体の体積の比は等しいという原理。

出典　小学館

ブリタニカ国際大百科事典 小項目事典

カバリエリの原理
カバリエリのげんり
principle of Cavalieri

曲線で囲まれた2個の平面図形を A，B とする。これらをある定直線に平行な直線で切れば，A，B で切取られた線分の長さの比が，常に a：b (一定) になるとする。このとき A，B の面積の比も a：b である。この定理はイタリアの数学者 B.カバリエリが実験的に発見した (1629) もので，立体についても，同様のことがいえる。すなわち，「2つの立体を A，B とする。一定の平面に平行な平面でこれらを切ったとき，その切り口の面積の比が常に a：b であれば，それらの体積の比も a：b である」。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

カバリエリの原理
かばりえりのげんり

二つの立体において、一平面に平行な平面で切った切り口の面積がつねに等しければ二つの立体の体積は等しい、という原理。イタリアのカバリエリがこの原理を発見し、微分積分法以前に、たとえば錐体(すいたい)の体積はつねに柱体の体積の3分の1に等しいことなどを発見した。

［竹之内脩］

カバリエリの原理

出典　小学館　日本大百科全書(ニッポニカ)

世界大百科事典（旧版）内のカバリエリの原理の言及

【カバリエリの定理】より

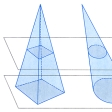
…平面上に二つの図形A,Bがあって，一定の方向の直線で両図形を切るとき，Aの切口の長さがつねにBの切口の長さのk倍であるならば，Aの面積はBの面積のk倍である。ガリレイの弟子B.カバリエリが，この事実を用いて種々の図形の面積を求める問題を論じたのは，微積分の発見される以前のことであって，この事実をカバリエリの定理(またはカバリエリの原理)という。このことを用いると，例えば，円x²＋y²＝a²の面積がπa²であることから，楕円x²/a²＋y²/b²＝1の面積がπabであることが導かれる。…

※「カバリエリの原理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」