日本大百科全書(ニッポニカ) 「ジョルダンの曲線定理」の意味・わかりやすい解説
ジョルダンの曲線定理
じょるだんのきょくせんていり
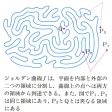
平面上の曲線の位相的性質に関する定理。円周と同位相な位相空間をジョルダン曲線Jという。すなわちジョルダン曲線とは、ある点から出発して、自分自身とはけっして交わらずに進み、最後に出発点へと戻る曲線のことである。よって、平面上の円周Sももちろんジョルダン曲線であるし、のような複雑な曲線Jもジョルダン曲線である。
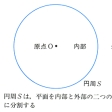
円周Sの場合、平面は円周によって、原点Oを含んでいる内部と、外へ無限に広がる外部との二つの部分に分けられる()。この性質が一般のジョルダン曲線でも成り立つことを主張するのが、ジョルダンの曲線定理である。すなわち「平面R2内のジョルダン曲線Jは、R2を内、外二つの領域G1とG2とに分ける」。つまり、R2-J=G1∪G2であり、さらにJは領域G1とG2の共通の境界となる(すなわちJ上の任意の点はG1からでもG2からでも到達できる)。
したがって、外部の1点から内部の1点へと曲線で結べば、かならずジョルダン曲線Jと少なくとも1回は交わる。一般には2点を結ぶ曲線がジョルダン曲線と奇数回交われば、それら2点は異なる領域に属し、偶数回交われば、それらは同じ領域に属することがわかる。
このジョルダンの曲線定理は、フランスの数学者ジョルダンがその『解析学講義』(1893)で述べたのが始まりであるが、その事実は直観的には古代の人々にも明らかであったので、人々は囲いに動物を追い込んでこれをとらえることができたのである。しかし、この証明は非常にむずかしく、完全な証明は20世紀に入ってから与えられた。また、ブローエルLuitzen Egbertus Jan Brouwer(1881―1966)やアレクサンダーJames Waddle Alexander(1888―1971)はこれを高次元へ拡張した。すなわち、「Jn-1がn次元ユークリッド空間Rn中のn-1次元球面であると、Rn-Jn-1は二つの成分G1とG2よりなり、Jn-1はG1とG2との共通の境界となる」。
[野口 廣]