改訂新版 世界大百科事典 「ボレル集合」の意味・わかりやすい解説
ボレル集合 (ボレルしゅうごう)
Borel set
n次元ユークリッド空間Rnにおいて,1点xからの距離がある正の数rより小さい点の全体を,xを中心とする半径rの開球という。開球の任意個数(有限個でも無限個でもよい)の合併として表される集合を開集合といい,開集合Gの余集合F=Rn-Gを閉集合という。Rnにおける開集合はたかだか可算無限個の開球の合併で表されることが知られている。開集合の任意個数の合併は開集合であるが,開集合の可算無限個の共通部分は必ずしも開集合でない。閉集合の任意個数の共通部分は閉集合であるが,閉集合の可算無限個の合併は必ずしも閉集合でない。そこでÉ.ボレルは1898年に次の概念を導入した。Rnの部分集合の族Bがボレル系であるとは,(1)Bに属する集合Eの補集合Rn-EはBに属する,(2)Bに属する可算無限個の集合E1,E2,……,Ek,……の合併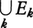 も共通部分
も共通部分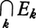 もBに属するという条件を満たすことである。とくにすべての開集合およびすべての閉集合を含むボレル系の中で最小のものをB0とするとき,B0に属する集合をボレル集合という。ボレル集合は測度,積分論において重要な概念である。
もBに属するという条件を満たすことである。とくにすべての開集合およびすべての閉集合を含むボレル系の中で最小のものをB0とするとき,B0に属する集合をボレル集合という。ボレル集合は測度,積分論において重要な概念である。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

