改訂新版 世界大百科事典 「積分論」の意味・わかりやすい解説
積分論 (せきぶんろん)
theory of integral
現代の積分論は空間の座標や位相の概念から離れて構成されるが，これはユークリッド空間におけるルベーグ積分の抽象化である。
ユークリッド空間におけるルベーグ測度は面積や体積の概念の拡張であって，空集合や全空間は明らかに可測集合（ルベーグ測度が定義される集合）であり，可測集合の和，差，交わりを作る操作をたかだか可算無限回行って得られる集合は可測集合である。また可測集合Eのルベーグ測度をm（E）と書くと，どの二つも互いに交わらない可測集合の可算無限列｛En｝に対して，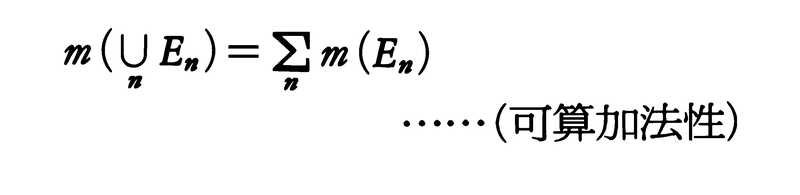
が成り立つ。
これらのルベーグ測度の性質から，一般の空間Xにおける測度の概念を次のように定義する。Xの部分集合の族Bがあって，（1）空集合φはBに属する，（2）E∈BならばX－E∈B，（3）En∈B（n＝1，2，……）ならば，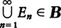
の3条件を満たすとき，Bを可算加法族，またはσ-加法族という。このときX∈Bであり，Bに属する集合の和，差，交わりを作る操作をたかだか可算無限回行って得られる集合はBに属する。よってBは上に述べた可測集合全体の族のようなものである。Bに属する集合Eに対して定義された関数（集合関数）μ（E）があって，（1）0≦μ（E）≦∞，空集合φに対してはμ（φ）＝0，（2）どの二つも互いに交わらない集合列En∈Bに対しては，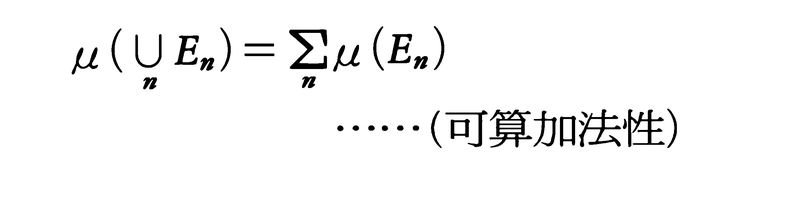
を満たすとき，μを（X，B）の上の測度という（これは前述のルベーグ測度mの概念に対応する）。Bに属する集合Eの上で定義された実数値関数f（x）について，任意の実数aに対してf（x）＞aなるEの点xの全体からなる集合がBに属するとき，f（x）はB-可測，または単に可測であるという。f，gが可測ならば，｜f｜，af＋bg（a，bは実数），fgは可測であり，g≠0なる点に制限して考えればf/gも可測である。またfn（n＝1，2，……）が可測であるならば，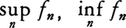
も可測であり，
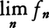が存在すればこれも可測である。集合E（∈B）上で可測な関数fの積分を次のように定義する。fが有界で負の値をとらないときは，Eを有限個の集合En∈Bの直和に分割してf（x）のEn上での値の下限をanとし，この分割⊿に対応する近似和，
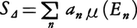を作る。あらゆる分割⊿に対するS⊿の上限をfのE上での定積分の値と定義して，
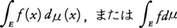と書く。fが有界でないときはfn（x）＝min｛f（x），n｝として，
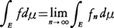と定義する。この積分の値が有限のときfはE上で可積分であるという。一般の実数値関数fに対しては，f⁺＝max｛f，0｝，f⁻＝max｛－f，0｝とするとf⁺，f⁻も可測で，
f＝f⁺－f⁻ （f⁺≧0，f⁻≧0）
となるから，f⁺，f⁻の少なくとも一方が可積分のとき，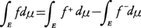
と定義する。この
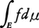が有限のときfは可積分であるという。Eで可測な関数の列｛fn｝があって，
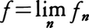が存在し，別にEで可積分な関数gがあってE上で｜fn（x）｜≦g（x）（n＝1，2，……）ならば，
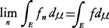が成り立つ（ルベーグの収束定理）。
二つの空間X1，X2において，それぞれの部分集合のσ-加法族B1，B2があり，（X1，B1），（X2，B2）の上にそれぞれ測度μ1，μ2があるとする。直積空間X＝X1×X2の部分集合でE＝A×B（A∈B1，B∈B2）の形の集合をすべて含む最小のσ-加法族をBとし，（X，B）において直積測度μ＝μ1×μ2を，上述のEの形の集合に対してはμ（E）＝μ1（A）μ2（B）となるように定義する。その方法は，二次元ユークリッド空間におけるルベーグ測度が，座標軸に平行な辺をもつ長方形に対しては縦と横の長さの積（すなわち二つの一次元ユークリッド空間でのルベーグ測度の積）として定義され，これから一般の集合に拡張されるのと同様な考え方による。X＝X1×X2の点をx＝（x1，x2）（x1∈X1，x2∈X2）のように表し，dμ1（x1），dμ2（x2），dμ（x）をそれぞれdx1，dx2，dxと書くことにする。X上の関数f（x）≡f（x1，x2）がB-可測であって，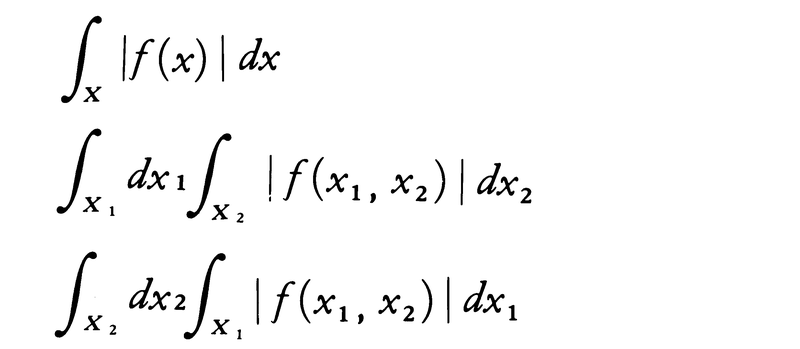
の三つのうちどれか一つが有限なら他の二つも有限で，その値は三つとも相等しく，そのとき次の等式が成立する（フビニG.Fubiniの定理）。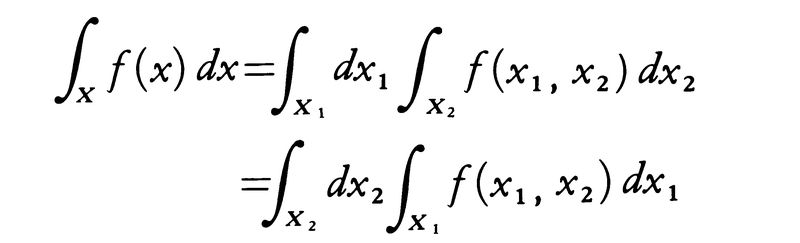
空間Xとその部分集合のσ-加法族Bがあって，Bで定義された有限な実数値（負の値でもよい）をとる集合関数F（E）が，上に述べた測度μの性質（2）と同じ可算加法性をもつとき，Fを（X，B）上の加法的集合関数という。別に（X，B）上の測度μがあって，μ（E）＝0ならばF（E）＝0となるとき，Fはμに関して絶対連続であるという。μに関して絶対連続な加法的集合関数Fに対して，X上で可積分な関数fが存在して，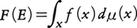
と表される（ラドン=ニコディムRadon-Nikodymの定理）。
このようにして構成された積分論は現代の解析学や確率論において欠くことのできない道具となっているので，現在では数学の基礎知識として，積分論といえばこのような一般の空間Xにおける測度の概念に基づく積分論を指すようになっている。
→測度 →ルベーグ積分
執筆者：伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報