ルジャンドル関数（読み）ルジャンドルかんすう（その他表記）Legendre function

改訂新版　世界大百科事典

ルジャンドル関数 (ルジャンドルかんすう)
Legendre function

nを0または正の整数とするとき，2階の線形微分方程式，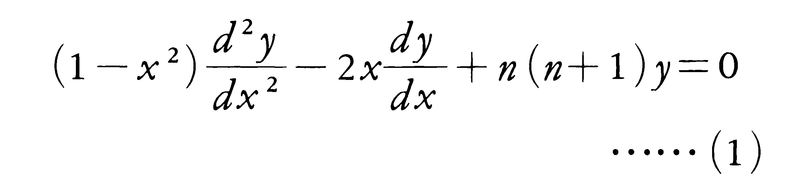

をルジャンドルの微分方程式といい，その解を一般にn次のルジャンドル関数という。また，mを正の整数とするとき，（1）を拡張して得られる常微分方程式，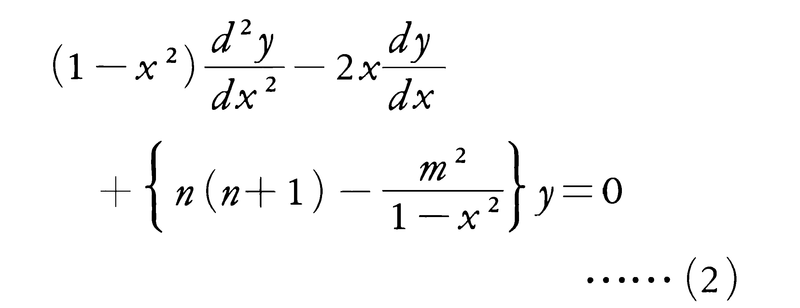

をルジャンドルの陪微分方程式といい，その解をルジャンドルの陪関数という（上の各微分方程式およびそれぞれの解となる関数は，nとmを任意の複素数としても定義されているが，本項目では，nとmは整数でn≧0，m＞0として述べる）。微分方程式（1）は下記のn次多項式P_n（x）および｜x｜＞1で収束する無限級数Q_n（x）の形の解をもつ。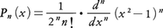

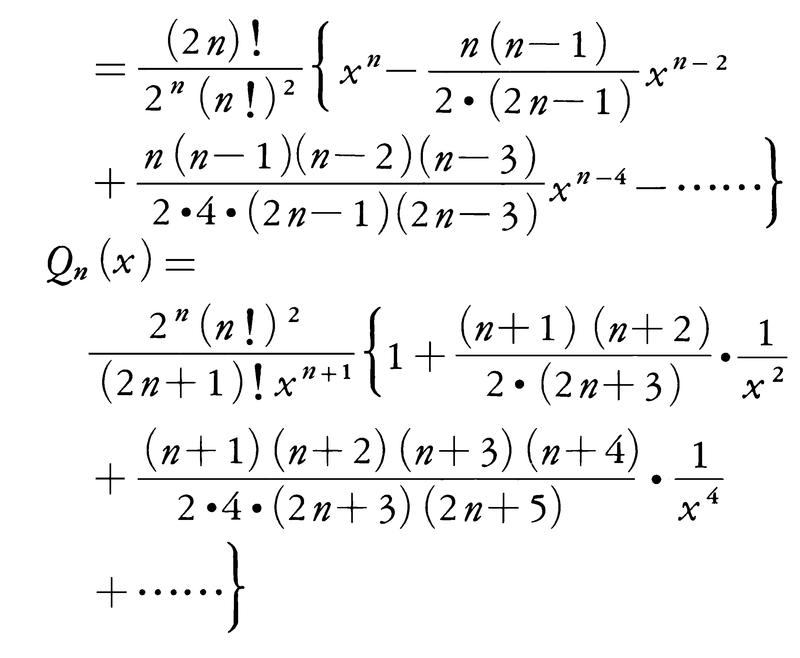
P_n（x）をルジャンドルの多項式または第1種のルジャンドル関数といい，Q_n（x）を第2種のルジャンドル関数という。微分方程式（2）は，P_n（x），Q_n（x）に対応して，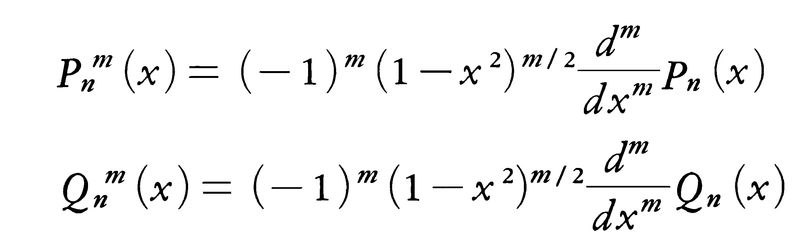

なる解をもつ。これらをそれぞれ第1種，第2種のルジャンドルの陪関数という。任意のmに対して｛P_n^m（n≧m）｝には直交関係，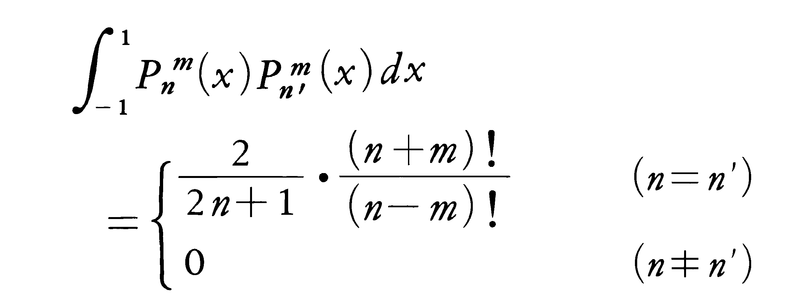

がある。ここで形式的にm＝0とおいて得られる｛P_n（n≧0）｝の直交関係も成立する。応用例としては，例えば三次元ラプラス方程式⊿U＝0を，極座標（γ，θ，φ）により，

　U＝u（γ）v（θ）w（φ）　……（3）　

と変数分離して解くと，u＝γⁿ，γ⁻ⁿ⁻¹;v＝P_n^m（cosθ），P_n^m（sinθ）;w＝cosmφ，sinmφとなる。ここでu，v，wの各二通りの関数からどのように選んで（3）の積を作っても，ラプラス方程式の解Uを得る。このように，ルジャンドル関数は，ポテンシャル，拡散，波動，量子力学などの問題を極座標を使って扱うとき，球面上の座標θに関する因子として現れるので，球関数とも呼ばれ，ベッセル関数と並んで数理物理学上重要な関数である。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」