球関数（読み）きゅうかんすう（英語表記）spherical functions

改訂新版　世界大百科事典

球関数 (きゅうかんすう)
spherical functions

数理物理学における微分方程式の解として登場する特殊な関数を総称して特殊関数と呼ぶが，なかでも球関数は簡単な式で表され，かつ種々の解析的な特性をもっている重要な例である。それはもっとも基本的な2階微分作用素であるラプラシアンΔに関係する。3変数x，y，zのときは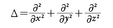，　であり，Δu（x，y，z）＝0となる関数uを調和関数という。適当な領域で温度分布uを考えたとき，定常状態ならそれは調和関数である。いま全空間で考えることとし，x，y，zの多項式でかつ調和関数であるものを系統的にさがし出そう。n次斉次多項式である調和関数をu_nとかく。このu_nを極座標x＝rsinθcosφ，y＝rsinθsinφ，z＝rcosθ（r＞0，0≦θ≦π，0≦φ＜2π）を用いて，

　u_n（x，y，z）＝rⁿY_n（θ，φ）

とかいたとき，Y_nがn次球関数である。それは球面上の関数とみることができ，各n≧0について2n＋1個の一次独立なn次球関数が存在する。それらはまた球面上のラプラシアン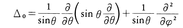，の固有関数として，

　Δ₀Y_n（θ，φ）＝－n（n＋1）Y_n（θ，φ）

のように特徴づけられる。

　ルジャンドル多項式P_n（x）（n≧0，｜x｜≦1）も特殊関数の一種で，次の式で定められる。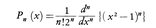　これはn次多項式で微分方程式，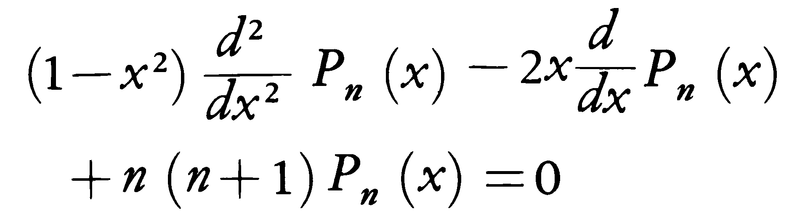

を満たす。

　さらにこのP_n（x）に従属した関数として，陪関数P_n、_m（x）（ただしP_n、₀（x）＝P_n（x））がある。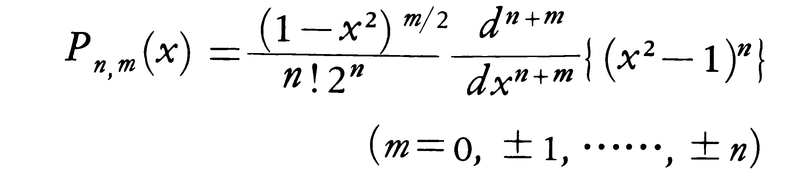

　n次球関数全体のなす2n＋1次元ベクトル空間の基底として，上記P_nm（x）を用いた系P_n（cosθ）_,P_nm（cosθ）cosmφ，P_nm（cosθ）sinmφ（0＜m≦n）をとることができる。これらは，曲面積要素dσ＝sinθdθdφについて互いに直交（積のdσによる積分が0）する。

　さらに球面上のdσについて2乗可積分な関数f（θ，φ）は，球関数によって，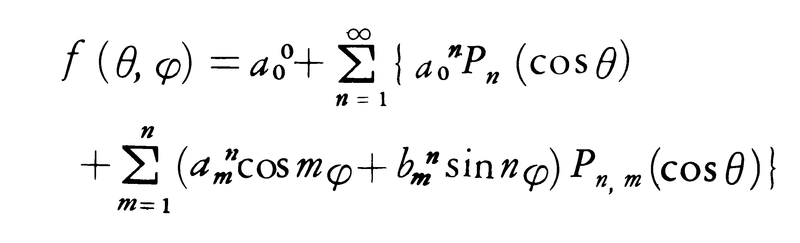

のように直交展開が可能である。これらの事実は，球についてディリクレ問題やノイマン問題の解法に有効な手段となり，また回転群のユニタリ表現を構成するときの基礎概念を与え，量子力学においては中心力場の電子に対するシュレーディンガー方程式の取扱いに現れるなど広い応用がある。
執筆者：飛田 武幸

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

球関数
きゅうかんすう
spherical function

球面調和関数ともいう。ラプラスの微分方程式 ΔU＝0 の解で，n 次 ( n は0または正の整数) の同次多項式であるもの U_n(x，y，z) は，球座標 を用いて表わせば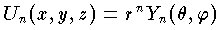， という形になる。この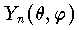右辺における を n 次の球関数という。これは t＝ cos θ とするとき，t に関する n 次のルジャンドルの多項式あるいはその随伴関数と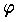， の三角関数で表現される。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の球関数の言及

【ルジャンドル関数】より

…ここでu,v,wの各二通りの関数からどのように選んで(3)の積を作っても，ラプラス方程式の解Uを得る。このように，ルジャンドル関数は，ポテンシャル，拡散，波動，量子力学などの問題を極座標を使って扱うとき，球面上の座標θに関する因子として現れるので，球関数とも呼ばれ，ベッセル関数と並んで数理物理学上重要な関数である。【伊藤 清三】。…

※「球関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」