化学辞典 第2版 「剛体球模型」の解説
剛体球模型
ゴウタイキュウモケイ
rigid sphere model
分子間相互作用を考えるとき,ファンデルワールス半径以下では無限大,以上では0の井戸型ポテンシャルで置き換えたモデルで,分子が接触したときだけ分子間に無限大の斥力がはたらく.実在気体の状態方程式,気体の衝突,懸濁液中でのコロイド粒子のふるまい,高分子溶液中における溶質-溶媒間相互作用,あるいは高分子溶液中における溶質-溶質間相互作用などにおける,排除体積効果に広く用いられている.高分子溶液の場合,溶質-溶媒間相互作用の記述には,半径として慣性半径が用いられる.このモデルでは,糸まり状高分子のセグメントで囲まれた溶媒分子が流体力学的相互作用によって,高分子と一体になって運動しているとする.この反対が剛体すぬけ分子(すぬけ効果)のモデルである.剛体球に関するアインシュタインの粘度式を用いて,極限粘度数[η]は次式で表される.
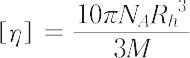
ここで,NA はアボガドロ定数,Mは分子量,Rh は剛体球の半径である.高分子鎖の溶液中における回転半径が Rh の値に近い実験事実から,溶媒が糸まり状高分子鎖の球体のなかを通り抜けられない非すぬけ分子である.すなわち,糸まり状高分子鎖の外側分子のみが流体の摩擦抵抗をうける剛体球とみなせる.分子量が数万以上の高分子では,一般に非すぬけ状態にある.[別用語参照]高分子溶液論
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報

