定幅曲線（読み）ていふくきょくせん

日本大百科全書(ニッポニカ)

定幅曲線
ていふくきょくせん

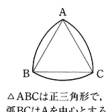
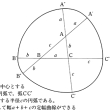
閉じた平面凸曲線が平行2直線l、mの間に収まっていて、かつl、mのいずれとも共有点をもつとき、l、m間の距離をこの曲線のl方向の幅という。方向に関係なく幅が一定である平面凸曲線を定幅曲線という。円は定幅曲線であるが、定幅曲線は円以外にもたくさんある。リューローReuleauxの三角形はその例である。同様の方法で一般に奇数個の頂点をもつ正多角形から定幅曲線をつくることができる。こうしてつくった定幅曲線はいずれも頂点のところがすこしとがっているが、至る所滑らかな定幅曲線をつくることもできる。縁が定幅曲線であるような硬貨（このような硬貨で円くないものが実際にイギリスなどにある）を自動販売機などのスリットに入れるときは、スリットの長さが硬貨の幅と同じなら、硬貨をどの部分から押し込んでもきっちり入る。また、この硬貨を平らな地面に垂直に立てたまま板を乗せて水平に転がすとき、硬貨の動きは複雑であるが、板のほうは高さを一定に保ちながら動く。幅がdの定幅曲線の周長は、曲線の形状に関係なくつねにπdであることが知られている。なお、定幅曲線と同じ要領で、空間の定幅曲面も定義できる。やはり、球面以外にも定幅曲面はたくさんある。たとえば、リューローの三角形をつくったような方法で、正四面体から定幅曲面をつくることができる。

［高木亮一］

定幅曲線（リューローの三角形）

定幅曲線（至る所滑らかな定幅曲線）

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

定幅曲線
ていふくきょくせん
curve of constant breadth

凸閉曲線（卵形線）を任意の平行な 2直線で挟むとき，その間の距離 d が常に一定であれば，この曲線を幅 d の定幅曲線という。ここに凸閉曲線とは次のような曲線のことである。平面上の無限に延びない領域 D があるとき，その中の任意の 2点を結ぶ線分が常に D に属すれば，この D を凸領域といい，凸領域の境界をつくる曲線を凸閉曲線という。円は凸閉曲線であり，また定幅曲線である。円のほかにも定幅曲線は無限に存在する。一例は正三角形の各頂点を中心として他の 2頂点を通る 3個の円弧で囲まれたルーロー Reuleauxの三角形である。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の定幅曲線の言及

【卵形】より

…方向を変えたときのCの幅の最大値，最小値をそれぞれCの直径，厚さという。幅が方向によらず一定である卵形線を定幅曲線という。幅がbである定幅曲線の周の長さはbπで，この中で最大の面積を囲むものは円であり，最小の面積を囲むものはルーローの三角形，すなわち正三角形の各頂点を中心とし辺の長さを半径とする円の各頂角に対する劣弧で作られる卵形線である。…

※「定幅曲線」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」