正多角形（読み）セイタカクケイ（英語表記）regular polygon

デジタル大辞泉

せい‐たかくけい【正多角形】

各辺の長さが等しく、内角の大きさがすべて等しい多角形。正多辺形。

出典　小学館

精選版 日本国語大辞典

せい‐たかっけい‥タカクケイ【正多角形】

1. 〘 名詞 〙 辺の長さおよび角の大きさがすべて等しい多角形。正多辺形。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

正多角形 (せいたかくけい)
regular polygon

平面上の多角形で，すべての辺の長さが等しく，またすべての内角の大きさも等しいものを正多角形といい，辺の個数がnである正多角形を正n角形または正n辺形という。正n角形の一つの内角の大きさは（2n－4）/n直角である。正多角形にはすべての頂点を通る一つの円（外接円）と，すべての辺に接する一つの円（内接円）がある。これらは同心円で，その中心は正多角形の中心と呼ばれる。円周をn等分して等分点を順次に結べばこの円を外接円とする正n角形が得られ，等分点で円に接線をひけばこの円を内接円とする正n角形が得られる（図1）。前の正n角形の周の長さをp_n，後の正n角形の周の長さをq_nとするとき，関係式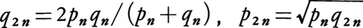，が成り立つ。これらを用いて，例えばn＝6から出発して順次n＝12，24，48，96，……に対するp_nとq_nを計算すれば，はじめの円周の長さはつねにp_nとq_nの間にはさまれているので，これより円周率の近似値とその誤差の範囲を求めることができる。正n角形は円周のn等分点をつくることによって得られるが，n等分点の作図は定規とコンパスの有限回の使用でできるとは限らない。nが形2^k×3×5 のときにこれが可能であることはユークリッド以来知られていたが，1796年にC.F.ガウスによって，これが可能であるnは，2^k×（相異なるフェルマー素数の積）の形に書けるものだけであることが示された。ここにフェルマー素数とは形2^k＋1 の素数のことである。例えば，n＝7，9，11，13，14に対しては作図不能で，n＝17に対しては作図可能である。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

正多角形
せいたかくけい

すべての辺が等しく、すべての内角も等しい多角形を正多角形という。正多角形は、円周を等分した点を順々に結んでできる多角形でもある。この円の中心を正多角形の中心という。この円は正多角形の外接円である。また正多角形には、その中心を中心として内接円をかくこともできる。辺の個数、したがって頂点の個数がnである正多角形を正n角形という。正四角形を普通、正方形という。正n角形は、各辺の両端と中心とを結んでn個の二等辺三角形に分けられる。その頂角は360度のn分の1である。正n角形は、その中心の周りのn分の360度の回転によって自分自身に重なる。すなわち、正n角形はn分の360度回転対称な図形である。nが偶数のときはその中心に関して点対称、すなわち180度回転対称な図形である。正n角形はすべてn個の線対称の軸をもっている。その対称軸は、nが奇数のときはn個の辺の垂直二等分線で、それぞれ一つの頂点を通る。nが偶数のとき線対称の軸は各辺の垂直二等分線および相対する頂点を結ぶ直線である。

　正n角形の作図は、円周をn等分することにほかならない。これを円周等分問題という。C・F・ガウスが19歳のとき正17角形の作図に成功したことは有名。円周等分問題はその後ガウスにより完全に解決された。その結果、nが7、9、11、13、14、18などの場合は、定規(じょうぎ)とコンパスで円周を等分することはできないことが明らかにされた。

　正三角形、正方形、正六角形のタイルのうち、どれか1種類を用いて平面を埋め尽くすことができる。1種類の正多角形でタイル張りができるのはこの三つだけである。2種類以上の正多角形によるタイル張りはいろいろとあり、各頂点に集まるようすが一様なものは11種あることが知られている。

［柴田敏男］

[参照項目] | 円周等分多項式

正多角形の例

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

正多角形【せいたかくけい】

辺の長さと内角の大きさがすべて等しい多角形。n個の頂点をもつ正多角形を正n角形という。一つの正n角形のすべての頂点を通る円（外接円）がただ一つ存在し，その中心をこの正n角形の中心という。正n角形は中心に関して対称で，正n角形はすべて互いに相似である。→正多面体

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

正多角形
せいたかくけい

「多角形」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典