接平面（読み）セツヘイメン（英語表記）tangent plane

デジタル大辞泉

せつ‐へいめん【接平面】

曲面上の一点で、この曲面に引いた接線をすべて含む平面。

出典　小学館

精選版 日本国語大辞典

せつ‐へいめん【接平面】

1. 〘 名詞 〙 曲面上の一点においてその曲面に接触する平面。曲面Ｓ上の点Ｐにおけるあらゆる接線が一平面ｐ上にあるとき、この平面ｐをＳのＰにおける接平面という。また、このとき、ｐはＰにおいてＳに接するともいう。

出典　精選版 日本国語大辞典

ブリタニカ国際大百科事典 小項目事典

接平面
せつへいめん
tangent plane

曲面 S を定義する関数 x＝x(u，v) ，y＝y(u，v) ，z＝z(u，v) がその定義域のすべての点で連続ですべて連続微分可能，すなわち S がなめらかであるとし，また S 上の1点をP ，P の座標を (x₀，y₀，z₀) とする。P における S の接平面とは，次の方程式を満たす平面のことである。
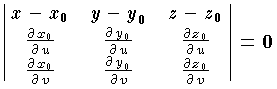ここで x₀＝x(u₀，v₀) ，y₀＝y(u₀，v₀) ，z₀＝z(u₀，v₀) である。この方程式は，λ，μ を媒介変数として x＝x(u，v)＋λ(∂x/∂u)＋μ(∂x/∂v) のベクトル方程式で表わすこともできる。この式から，接平面は，点Pを通る曲面上の曲線の接線ベクトル ∂x/∂u，∂x/∂v によって決定される平面であることがわかる。このときの点P を接点，P における接平面上のベクトルを接ベクトルまたは曲面上のベクトルという。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

接平面 (せつへいめん)
tangent plane

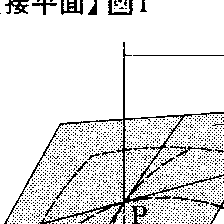
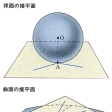
Sをなめらかな曲面とし，PをS上の点とする。このとき，Pを通るS上の曲線を任意にとり，Pにおけるこの曲線の接線をつくれば，これらはすべて同一平面上にある。この平面を点Pにおける曲面Sの接平面と呼び，Pをその接点と呼ぶ。なお，Pにおいて接平面に立てた垂線を点Pにおける曲面Sの法線という（図1）。点Pが中心をOにもつ球面上にあるとき，Pにおける接平面はPを通り半径OPに垂直な平面である。この場合は曲面は接平面の片側だけにあるが，一葉双曲面の例が示すように，つねにそうであるとは限らない（図2）。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

接平面
せつへいめん

中心がOの球面上の点Aで半径OAに垂直な平面は、この球面と点Aだけを共有している。この平面を球面の接平面といい、Aを接点という。一般の曲面Sでは、その上の点Aを通ってS上に引いた任意の曲線にAで接線を引くと、これらの接線がすべて同上の平面上にあるとき、その平面を点Aでの曲面Sの接平面という。したがって円錐(えんすい)面の頂点のようなところでは接平面は存在しない。また、接平面と元の曲面との共有点は一つとは限らない。たとえば、円柱面の接平面は母線を含んでいる。

［栗田　稔］

球面と曲面の接平面

出典　小学館　日本大百科全書(ニッポニカ)