日本大百科全書(ニッポニカ) 「数値積分法」の意味・わかりやすい解説
数値積分法
すうちせきぶんほう
numerical integration
関数の定積分の値を、解析的方法によらず、数値的に近似計算する方法の総称。解析的に計算できない問題にも広く適用できるので、実務に多く用いられる。また、計算の手続が比較的単純なので、コンピュータ処理に適している。数値積分法の原理は、積分区間をいくつかの小区間に分け、各小区間のうえで被積分関数を簡単な式(普通は補間多項式)で近似し、近似式の積分値を加え合わせる、ということにある。公式としては中点公式、台形公式、シンプソンの公式などが簡単でよく用いられている。より高精度の公式として、ニュートン‐コーツの公式、ガウス型の公式がある。そのほか、重積分の公式、無限区間上の積分の公式、自動積分公式(計算式や分点数などを関数と指定精度にあわせて自動調節する公式)などがある。
[戸川隼人]
簡単な公式の例
台形公式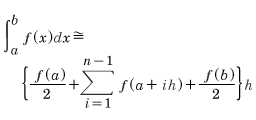
シンプソンの(第一)公式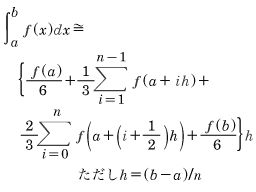
[戸川隼人]
公式の選び方
普通は、十分に細かい分割をして、台形公式を適用するのが無難である。次数の高い近似を用いる公式は、理論上の精度は良いが被積分関数が十分に滑らかで、関数値を精度良く計算できることを前提にしているので、使い方が適切でなければ副作用がでる。
[戸川隼人]
分割数の決め方
分割が粗すぎれば離散化誤差が大きくなる。一方、分割が細かすぎれば丸め誤差の累積のために精度が悪くなる。良い精度を得るには分割数をうまく選ぶ必要があるが、もっとも適切な分割数を先験的に知ることはむずかしいので、たとえば100等分、1000等分、1万等分、というように何段階かの細かさで計算してみることが望ましい。
[戸川隼人]
『津田孝夫著『計算機による多変数問題の数値解析』(1973・サイエンス社)』▽『デービス、ラビノビッツ著、森正武訳『数値積分法』(1980・日本コンピュータ協会)』▽『森正武著『FORTRAN77 数値計算プログラミング』(1987・岩波書店)』▽『杉浦洋著『数値計算の基礎と応用――数値解析学への入門』(1997・サイエンス社)』▽『星守・小野令美・吉田利信著『入門数値計算――チャートによる解説とプログラム』新版(1999・オーム社)』

