精選版 日本国語大辞典 「ガウス」の意味・読み・例文・類語
ガウス
日本大百科全書(ニッポニカ) 「ガウス」の意味・わかりやすい解説
ガウス(Karl Friedrich Gauss)
がうす
Karl Friedrich Gauss
(1777―1855)
ドイツの数学者。ブラウンシュワイクに生まれる。家は貧しかったが、幼時より数学、語学などに並はずれた才能を示す神童であった。教育施設の比較的良好であったブラウンシュワイク公国で、教師にも恵まれ、14歳のときに領主フェルディナンド公爵(1735―1806)の前で行った暗算の妙技は、公爵の心をとらえ、公爵が没するまでその手厚い庇護(ひご)を受けることになった。15歳でカロリナ高等学校に入学。17歳のとき購入したニュートンの『プリンキピア』でニュートン力学をマスターしたものと思われる。高校時代、そのすばらしい計算能力によって、数に関する数多くの性質を自力で次々と発見していた。
1795年10月、待望のゲッティンゲン大学に入学した。完備した大学の図書館で文献を調べてみると、彼の発見した事実の多くは、すでにオイラー、ラグランジュ、ルジャンドルらには既知のものであることがわかり、心穏やかではなかったが、一方、これら先哲の考えを上回る諸発見もあり、大いに力を得た。研究を続けるうち、1796年3月29日の朝、次のような新事実を発見した。
「方程式xp-1=0の虚根は、pがp=2m+1(m=2k)の形の素数ならば、平方根だけが混ざっている有理式で表せる。すなわち幾何学的に言い表すと、pがこの形ならば、正p角形は定規(じょうぎ)とコンパスだけの使用で作図可能である。とくにk=2ならばp=17となり、したがって正十七角形は作図可能である。」
これはユークリッド以来2000年間、だれもが夢想だにしなかった素人(しろうと)うけのする新発見であった。実は、この定理を含む整数の組織的な研究が彼の本領であって、これは1801年の夏、画期的な『整数論』Disquisitiones arithmeticaeとして出版され、整数論の古典となった。
1801年元日、イタリアのピアッツィは、火星と木星の間を浮遊する小天体(のちにケレスと命名された小惑星の第一号)を発見したが、わずかの観測ののち姿を消し、天文学者の努力にもかかわらず所在不明となった。これを知ったガウスは、自分の案出した新計算法によって軌道を算出したが、同年の12月7日、予測どおりの位置にその小天体が再発見され、一躍天文学でも名声を博した。このときの理論は『天体運動論』(1809)として発表されている。このような業績によって、1807年、ゲッティンゲン大学の教授および天文台長として招かれた。これより先、大学時代に親友だったボヤイ・ファルカス(非ユークリッド幾何発見者の一人ボヤイ・ヤノスの父)からの影響で、ユークリッド幾何の平行線問題に深く関心をもつようになり、1816年ごろには「非ユークリッド幾何」(ガウスが命名した呼び方)の存在を信ずるようになった。1822~1830年ごろ、たまたまガウスはハノーバー地方の測量に携わるようになったときも、実測によってこの新幾何の存在を確かめようと考えたらしく、測地学研究の副産物である名著『曲面の一般研究』にこの問題の解決法に関する考えが込められていた。この曲面論は、のちにリーマンによってn次空間にまで拡張され、A・アインシュタインの「一般相対性理論」にまで発展することになる。
以上の著述のほか、最小二乗法、代数方程式の根(こん)の存在、超幾何級数、ポテンシャル論、電磁気学など、純粋数学だけでなく応用数学方面にも画期的な業績を残し、その後の数学の発展にきわめて大きな貢献をした。「寡なれど熟pauca sed matura」を堅持したガウスは、楕円(だえん)関数論などで時流を超えた研究を行ったが、未発表に終わったものが少なくない。これらは、未完の遺稿として貴重な研究日誌、知人への書信などとともに全13巻の全集に収められている。
[寺阪英孝]
『ダニングトン著、銀林浩・小島毅男・田中勇訳『ガウスの生涯』(1976/新装版1992・東京図書)』
改訂新版 世界大百科事典 「ガウス」の意味・わかりやすい解説
ガウス
Carl Friedrich Gauss
生没年:1777-1855
19世紀前半を代表するドイツの数学者。ブラウンシュワイクの貧しい家庭に生を受け,幼時から数計算に特異な才能を示した。ブラウンシュワイク公フェルディナントの後援を得て,1792年コレギウム・カロリヌムに進学,古典語,近代諸語を学ぶかたわら,I.ニュートン,L.オイラー,J.L.ラグランジュらの数学書に親しみ,95年には帰納的に二次の相互法則を発見した。同年秋ゲッティンゲン大学に入学。主として古典文献学,物理学に興味を示しつつ,ほぼ独力で数学を研究した。同大学の古典文献学教授。ハイネの影響もあって,当初は文献学者を目ざした。96年正十七角形の作図法を発見,98年にはゲッティンゲンを去り,翌年ヘルムシュテット大学から〈代数学の基本定理〉の証明などによって学位を得た。1801年,それまでの整数論研究を集成した画期的著作《数論研究》を刊行,新しく発見された小惑星ケレスの軌道計算の成功と相まって,数学上の名声を不動のものにした。07年,ゲッティンゲン大学天文台長のポストを供与され,これを受諾した。同大学では数学の講義も担当したが,内容はほとんど初等的なものであった。ベルリン大学開学の折には,数学教授に招請されたがこれを受けず,終生ゲッティンゲンにとどまることになった。19世紀初頭には,ボーヤイJ.やN.I.ロバチェフスキーに先立って,非ユークリッド幾何学の可能性を考え始めていたが公表は慎重に差し控えた。研究領域を純粋数学を超えて,天文学,測地学,電気・磁気学などに広げ,経験科学の分野に理論数学的問題を見いだした点にガウスの研究上の特徴が認められる。1830年代のW.ウェーバーとの実験物理学上の共同研究は著名である。ガウスはアルキメデス,ニュートンと比肩できる大数学者であったが,考案の横溢に比較して,発表には完全主義者の態度を保持し,19世紀前半のドイツ科学界で孤高の存在であった。54年,G.F.B.リーマンのゲッティンゲン大学就職講演〈幾何学の基礎をなす仮設について〉に出席し大きな印象を受けたと思われるが,それはまたガウスの時代の終焉(しゆうえん)をも刻印するものであった。
執筆者:佐々木 力
ガウス
gauss
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「ガウス」の意味・わかりやすい解説
ガウス
→関連項目アーベル|数値積分|デデキント
ガウス(単位)【ガウス】
→関連項目ガウス|テスラ(単位)
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「ガウス」の意味・わかりやすい解説
ガウス
Gauss, Carl Friedrich
[没]1855.2.23. ゲッティンゲン
ドイツの数学者。アルキメデス,アイザック・ニュートンと並び称される学者で,近代数学の創始者ともいわれている。幼少の頃から数学と古典語にぬきんでた才能を示し,ブラウンシュワイク公の保護のもとに勉強を続けた。 1795~98年ゲッティンゲン大学に学ぶ。 1807年ゲッティンゲン大学の天文台長兼数学教授となる。 1793~94年整数論の諸問題に取り組み,1794年に最小二乗法を発見,1801年にガウスの最大の業績といわれる『整数論考究』を発表,同年最小二乗法を駆使して準惑星ケレスの軌道計算を行ない,これを再発見した。数学,天文学以外にも,物理学,測地学など多分野にわたって業績を残した。
ガウス
Gauss, Clarence Edward
[没]1960.4.
アメリカの外交官。 1906年国務省に入り,07年上海領事館に勤務。その後上海,天津,アモイ,済南,奉天の領事あるいは総領事を歴任。北京公使館顧問をつとめたのち,上海総領事,オーストラリア駐在公使を経て,41年2月中国駐在大使となった。第2次世界大戦中,当初は国民政府に同情的であったが,のち批判的になり,内政改革と国内統一を主張したが,44年 11月 J.スティルウェル将軍が解任されたのを不満として大使を辞任。 45年国務省を退官した。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
最新 地学事典 「ガウス」の解説
ガウス
Gauss, Carl Friedrich
1777.4.30~1855.2.23 ドイツ ブラウンシュワイクの貧しい煉瓦職工の家に生まれ,ゲッチンゲン大学に学び,30歳のとき新設のゲッチンゲン天文台長となり研究に没頭した。数学・天文学・物理学などに幾多の業績があるが,測地学・地球電磁気学でも基礎的な仕事をした。参考文献:E.Worbs(1955) Carl Friedrich Gauss, ein Lebensbild, Koehler & Amelang
執筆者:藤井 陽一郎
ガウス
gauss
cgs系の磁束密度および磁化の単位。Gと表記。1GはSI系の磁束密度10-4T(テスラ)と,磁化4π×10-4T(E-B対応SI系では103A/m)にそれぞれ等しい。
執筆者:鳥居 雅之
出典 平凡社「最新 地学事典」最新 地学事典について 情報
単位名がわかる辞典 「ガウス」の解説
ガウス【gauss】
化学辞典 第2版 「ガウス」の解説
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
山川 世界史小辞典 改訂新版 「ガウス」の解説
ガウス
Karl Friedrich Gauss
1777~1855
ドイツの数学者。その業績は19世紀数学のあらゆる分野に及び,特に整数論,行列式論,最小自乗法,複素数の導入,ポテンシャル函数の研究などが著名である。
出典 山川出版社「山川 世界史小辞典 改訂新版」山川 世界史小辞典 改訂新版について 情報
旺文社世界史事典 三訂版 「ガウス」の解説
ガウス
Karl Friedrich Gauss
ドイツの数学者
整数論や曲面論,複素数の導入,小惑星の軌道計算など数学上優れた業績を残した。
出典 旺文社世界史事典 三訂版旺文社世界史事典 三訂版について 情報
367日誕生日大事典 「ガウス」の解説
ガウス
アメリカの外交官
1960年没
出典 日外アソシエーツ「367日誕生日大事典」367日誕生日大事典について 情報
世界大百科事典(旧版)内のガウスの言及
【幾何学】より
…第5公準を大胆にも否定して,それを〈直線外の1点を通りその直線に平行な直線は少なくとも2本ある〉という公準におきかえた幾何学を構成したのはN.I.ロバチェフスキーとボーヤイ J.で,それは1830年ころのことであった。当時の数学界の帝王C.F.ガウスもこのような幾何学の存在を信じ,それを非ユークリッド幾何学と呼んだが,騒々しい非難を恐れて未発表にしたことが後年になってわかった。しかしながら,これらの人たちは非ユークリッド幾何学を展開しただけで,その無矛盾性を証明したわけではなかった。…
【誤差】より
…測定,理論的推定,近似計算などの結果として得られた値と真実の値との差。諸量の測定値の誤差を数学的に取り扱う誤差論は,1800年代の初めにC.F.ガウスによって始められた。その主要な内容は彼自身によって完成されたといってよいほどで,同じガウスにより創始された最小二乗法と表裏をなすものである。…
【最小二乗法】より
…19世紀の初め,C.F.ガウスが天体の運動理論を展開するにあたって,多くの観測結果にもっともよく一致するよう軌道を決定するために開拓された方法であって,応用範囲も広く,誤差論と一対をなしている。 ある未知量を測定するのに,十分注意を払っても偶発的な誤差を免れない。…
【数学】より
…18世紀にはほとんどすべての数学者が応用に携わり,功利主義的な数学観が支配していたが,19世紀には〈ギリシアへの復帰〉の機運が見られるようになったのである。 C.F.ガウスは両世紀の境界に立つ数学者である。彼はゲッティンゲン大学の天文台長となって,みずから観測にも従事して,天文学,測地学,電磁気学など数学の応用にも著しい功績があったが,それに関連して最小二乗法を数学的に基礎づけたり,曲面論,ポテンシャル論を展開するなど,純粋数学の新生面をも開いた。…
【数理統計学】より
…確率論の発展はこの推論の方法に大きな影響を与えてきた。
【数理統計学の始まり】
C.F.ガウスとP.S.ラプラスは,すでに19世紀の初めに母数の推定法を論じている。ラプラスは,その研究において,母数の真の値θと推定値![]() との誤差を評価するのに絶対値|θ-
との誤差を評価するのに絶対値|θ-![]() |の単調関数を用いた。…
|の単調関数を用いた。…
【整数論】より
…このような疑問からオイラーは平方剰余の相互法則を発見した。この平方剰余の相互法則は,その後A.M.ルジャンドルによって再発見され,特別な場合の証明が与えられたが,完全な証明はC.F.ガウスが初めて与えた。またオイラーは,関数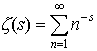 を考え,ζ(s)についていくつかの重要な性質を見いだした。…
を考え,ζ(s)についていくつかの重要な性質を見いだした。…
【代数学】より
…第2はF.ビエトらによる数式表示の革命,すなわち,それまで方程式は文章で表されていたのであるが,まずドイツで+,-の記号の使用が始まり,ビエトは+,-だけでなく,未知数を母音を表す文字で,係数を子音を表す文字で表して,文字係数の一般方程式を書き始めた。一方,三次方程式のG.カルダーノの解法においては,実根を求めるのに虚数が必要になることが当時の数学者を悩ませたが,18世紀のL.オイラーらが計算に虚数を使うようになり,やがて18世紀末から19世紀にかけてC.F.ガウスが複素数の重要性を明確にとらえて,ガウス平面の利用を含めて複素数を実在の数として数学者に意識させるようにした。ガウスを含む何人かの人々により複素数の体系が確立したことは,その後の数学の発展に非常に大きい貢献をした。…
【地球物理学】より
…19世紀の末,測地学は理論的にも計測的にも早くも精密科学としての形態をととのえた。地磁気学も1600年のW.ギルバートの《磁石について》あたりから経験科学の姿をとりはじめ,19世紀の半ばには碩学C.F.ガウスによって地磁気ポテンシャルの一般理論が展開され,理論的科学としても確立した。地震学は明治の初め(19世紀末),日本で外国人科学者による地震計観測が始められて初めて近代科学となった。…
【ガウス単位系】より
…メートル法に属する単位系の一種で,CGS単位系に分類されるが,電磁気に関係のあるさまざまな量のうち,電気的な量に対してはCGS静電単位系の単位を,一方,磁気的な量に対してはCGS電磁単位系の単位を用いる単位系である。例えば,電気的な量の一つである電荷に対しては,CGS静電単位系のcm3/2g1/2s-1を用い,磁気的な量の一つである磁束密度に対してはCGS電磁単位系のcm1/2g1/2s-1(これをガウス(G)と表すこともある)を用いる。折衷的な単位系ではあるが,それなりに実用上の便宜があるので,比較的広く使われてきた。…
※「ガウス」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

