無限集合（読み）ムゲンシュウゴウ

デジタル大辞泉

むげん‐しゅうごう〔‐シフガフ〕【無限集合】

数学で、元の数が無限である集合。

出典　小学館

精選版 日本国語大辞典

むげん‐しゅうごう‥シフガフ【無限集合】

1. 〘 名詞 〙 数学で、元の個数が無限である集合。自然数全体の集合・有理数全体の集合などはその例である。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

無限集合
むげんしゅうごう

無限個の元を含む集合をいう。無限集合は、いかなる自然数nに対しても、n個より多くの元を含む。これは無限集合の一つの定義である。自然数全体の集合と、これからゼロを取り除いた集合を考える。これらの二つの集合の間には、次のような一対一の対応をつけることができる。

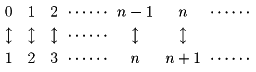
　自然数全体の集合は、偶数全体、あるいは奇数全体の集合とも一対一の対応をつけることができる。有限集合ではこのように、自分自身の真部分集合との間に一対一の対応をつけることはできない。デーデキントはこの特徴に着目して、無限集合を定義した。すなわち、「集合Aは、Aのある真部分集合A′と一対一の対応がつけられるとき無限集合という」。これがもう一つの定義である。

　これら二つの定義は、一見して同値な命題のようであるが、第一の定義から第二のものを導くには、選択公理が必要である。選択公理を用いれば、第一の無限集合は、自然数の全体と一対一の対応づけのできる部分集合をもち、第二の定義を満たすことがわかる。無限に対することばは有限である。無限集合でないものを有限集合と定義すれば、無限集合と有限集合は、一方は他方を否定したものとして定義することができる。

［西村敏男］

[参照項目] | 有限集合

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

無限集合
むげんしゅうごう
infinite set

元 (要素) の個数が無限である集合をいう。たとえば，自然数の集合{1，2，3，…，n，…}など，すべての有理数の集合，すべての実数の集合，直線上のすべての点の集合，平面上のすべての点の集合などは無限集合である。無限集合の特徴は，それと同等な真部分集合を含むことである。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の無限集合の言及

【集合】より

…このような濃度を有限の濃度という。(2)有限集合でない集合を無限集合といい，その濃度を無限の濃度という。(3)一般に，二つの集合A,Bについて，♯(A)と♯(B)との大小関係を次のように定める。…

※「無限集合」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」