選択公理（読み）せんたくこうり（英語表記）axiom of choice

改訂新版　世界大百科事典

選択公理 (せんたくこうり)
axiom of choice

選出公理ともいう。空集合φを含まない集合族（集合の集合）に対して，それに属する各集合からそれぞれ一つずつ元を一挙に選び出してそれらの全体がまた集合になるようにできるという集合論の命題である。換言すれば，集合族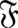に属する集合がいずれも空集合でないとき，すべてのF∈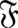に対して，f（F）∈Fを満たす写像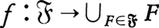が存在するという陳述である。このような写像fを選択関数という。G.カントルは〈いかなる集合もその元の間に適当に順序を定義して整列集合にすることができる〉（整列可能定理）が成り立つことを予想していたが，1904年，E.ツェルメロが選択公理を初めて提出し，これを用いて整列可能定理を証明した。選択公理は代数学や解析学において無意識のうちに用いられている場合が多い。選択公理と整列可能定理およびツォルンの補題の三つは互いに同等な命題であることが証明できる。ツォルンの補題とは次の命題をいう。Xを任意の順序集合とする。Xのいかなる全順序部分集合も上界をもてば，Xには少なくとも一つの極大元が存在する。ツォルンの補題は応用上便利であって，数学の多くの分野で選択公理や整列可能定理よりもよく用いられる。選択公理を用いて得られる重要な結果として，例えば（1）任意の二つの集合の濃度は比較可能である。（2）コンパクト空間の直積位相空間はまたコンパクトである。（3）ルベーグ非可測な集合が存在するなどがある。なお，選択公理は集合論の公理系から独立であることが証明されている。
執筆者：柘植 利之

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

選択公理
せんたくこうり

「ツェルメロの公理」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の選択公理の言及

【集合論】より

…カントルが集合と定義した内容のものは必ずしも集合ではないので，それを領域と呼ぶことがある。　また，公理のうちで，特別視されているものに選択公理がある。それは，〈ある集合Mの部分集合の集りNがあり，Nの各元は空集合でないとき，Nの各元sに対して，sの元を一つずつ対応させることができる〉というものであり，何となく当然のように聞こえるが，これを公理として取り上げる理由は，Nが非常に大きい濃度をもっているかも知れないので，〈ものすごい無限回の操作をいっぺんにすます〉という特殊なことを含んでいる。…

※「選択公理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」