立方体倍積問題（読み）りっぽうたいばいせきもんだい（英語表記）duplication of a cube

精選版 日本国語大辞典

りっぽうたいばいせき‐もんだいリッパウ‥【立方体倍積問題】

1. 〘 名詞 〙 古代ギリシアの幾何学における三大難問の一つ。「与えられた立方体の二倍の体積をもつ立方体を作れ」という作図題。一八三七年に作図不能であることが明らかにされた。立方倍積問題。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

立方体倍積問題
りっぽうたいばいせきもんだい
duplication of a cube
Delian problem

長さ1の線分が与えられているとき、³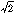　の長さの線分を定木とコンパスで作図せよ、という問題をいう。与えられた立方体の2倍の体積をもつ立方体を作図する問題であるから、このようによばれる。

　定木とコンパスで作図できる線分の長さは有理数体Q上2のべき次元線形空間の元であるのに、X³－2がQ係数の既約多項式で、³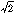　がQ上三次元線形空間の元であることにより、作図不可能が示される。

　古代ギリシアのデロス島の守護神アポロンが祭壇の2倍のものをつくれと命じたという神話からデロスの問題ともいわれ、ギリシアの三大作図不能問題の一つとして有名である。

［菅野恒雄］

[参照項目] | 作図不能問題

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

立方体倍積問題【りっぽうたいばいせきもんだい】

デロスの問題とも。〈与えられた立方体の２倍の体積をもつ立方体を作れ〉という問題。１辺の長さの（式１）倍を作図することに帰着し，定規とコンパスを使うだけでは作図不能。古代ギリシア以来の難問だったが，1837年P.L.ワンツェルが不可能なことを証明。→作図不能問題
→関連項目エウドクソス

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

立方体倍積問題
りっぽうたいばいせきもんだい

「デロスの問題」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の立方体倍積問題の言及

【エラトステネス】より

…この方法は自然数を小さい順に並べ，小さいほうの素数の倍数を次々に消去して素数を残していくという原始的なものである。さらに古代ギリシア数学の三大問題の一つ，立方体倍積問題にも取り組み，器械的な作図解を与えた。これは，長方形の枠に沿って，枠の幅に等しい高さの三つの平行四辺形が滑るようになっている装置によって，二つの比例関係を求めるものである。…

【作図不能問題】より

…古代ギリシアの幾何学者によって扱われた使用器具を定規とコンパスに限定する平面図形の作図がもっともよく知られているが，これに関する次の三つの問題がとくに著名である。(1)与えられた角を3等分すること(角の3等分問題)，(2)与えられた立方体の体積の2倍の体積をもつような立方体を作ること(立方体倍積問題)，(3)与えられた円と等しい面積をもつ正方形を作ること(円積問題)。これらの問題は前5,6世紀ごろからギリシアの幾何学者によって研究され，執拗（しつよう）にその解法が求められたのであるが，解決をみず，ギリシア数学の三大問題として後世に残された。…

※「立方体倍積問題」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」