作図（読み）サクズ

デジタル大辞泉

さく‐ず〔‐ヅ〕【作図】

［名］(スル)
１ 図面や図形を描くこと。「機械の設計図を作図する」
２ 幾何学で、定規とコンパスを使い、与えられた条件を満たす図形を描くこと。また、その図形。
[類語]製図

出典　小学館

精選版 日本国語大辞典

さく‐ず‥ヅ【作図】

1. 〘 名詞 〙
2. ① 図をかくこと。図をひくこと。
3. ② 幾何学で定規とコンパスを用いて、与えられた条件に適する図形を描くこと。また、その書いた図形。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

作図
さくず

与えられた条件を満足する図形をつくること。普通、初等幾何における作図というのは、定規（定木）(じょうぎ)とコンパス（円規）による作図のことであって、定規は2点を通る直線を引くことに、コンパスは与えられた点を中心として与えられた半径をもつ円をかくことに用いられる。そして、2直線の交点、直線と円の交点、円と円の交点を使って要求にあう点、直線、円、三角形などを作図する。作図の問題の理論的な扱いは、次の四つの段階に分けられる。

〔1〕解析　求めるものが得られたとして、それを作図する手掛りをみいだす。

〔2〕作図　得られた手掛りを基にして作図する方法を示す。

〔3〕証明　この方法で作図したものが要求にあうものであることを証明する。

〔4〕吟味　要求にあうものがいくつあるかを調べる。

［栗田　稔］

基本作図

(1)線分ABの中点、およびこの点を通ってABに垂直な直線（垂直二等分線）をつくること（図A）。(2)直線の上の点でこれに垂線を引くこと（図B）。直線外の点からこの直線へ垂線を引くこと。(3)角の二等分線をつくること（図C）。(4)与えられた半直線を一つの辺として、与えられた大きさの角をつくること（図D）。(5)直線外の点を通ってこの直線に平行な直線を引くこと（図E）。(6)与えられた三つの長さを3辺の長さにもつ三角形をつくること。(7)1直線上にない3点を通る円をかくこと（図F）。(8)与えられた線分を直径とする円をかくこと。(9)円周上の点でこれに接線を引くこと。(10)円外の点からこの円へ接線を引くこと（図G）。(11)与えられた線分を弦とし、これを与えられた大きさの角に見る円弧をかくこと（図H）。

［栗田　稔］

いろいろな作図法

〔1〕軌跡交会法　点Pについて与えられた条件C₁、C₂に分け、それぞれの条件を満たす点の軌跡の交点として点Pを求める。たとえば、3点A、B、Cから等距離にある点Pは、A、Bから等距離にある点の軌跡（線分ABの垂直二等分線）とB、Cから等距離にある点の軌跡（線分BCの垂直二等分線）の交点として求められる。

〔2〕図形の変換を利用する作図　移動を利用する作図法には、平行移動法、対称移動法、回転移動法がある。たとえば、3直線a、b、cが与えられているとき、cに垂直な直線を引いてa、b、cとの交点A、B、Cについて、Cが線分ABの中点になるようにするには、cについてaと対称な直線とbとの交点をBにとればよい。また、図形の拡大・縮小を利用する作図法は、相似法といわれる。たとえば、鋭角三角形の中へ、1辺を三角形の辺上に置いて内接する正方形をつくる（図I）。

〔3〕代数解析法　これは次のことを使う作図法である。(1)長さa、bを知って和、差を長さにもつ線分をつくること。(2)長さa、b、cを知って、長さab/cを求めること。(3)長さa、bを知って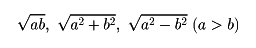

を長さとする線分を求めること。(4)長さa、bを知って、二次方程式
　　x²－ax＋b²＝0　(a≧2b),
　　x²－ax－b²＝0
を満たす正数xを長さにもつ線分を作図すること（図J）。たとえば、与えられた円に内接する正五角形、正十七角形などがこの方法で作図できる。一般にpが素数でp＝2ⁿ＋1（nは自然数）のとき、与えられた円に内接する正p角形は、定規とコンパスにより作図できる。

［栗田　稔］

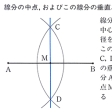
基本作図〔図A〕

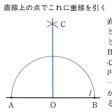
基本作図〔図B〕

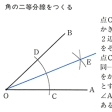
基本作図〔図C〕

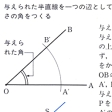
基本作図〔図D〕

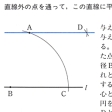
基本作図〔図E〕

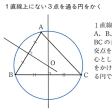
基本作図〔図F〕

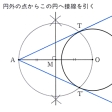
基本作図〔図G〕

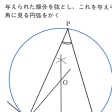
基本作図〔図H〕

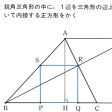
図形の変換を利用する作図（相似法）〔図…

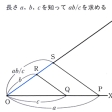
代数解析法〔図J〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

作図 (さくず)
geometrical construction

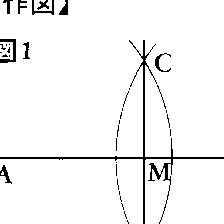
与えられた条件を満たす図形をある特定の器具だけを有限回使用して作ることを作図という。古くから有名なのはユークリッド以来の直線を引くための器具としての定規（距離を測ったりくぎったりするのに用いてはならない）と円を作るための器具としてのコンパスだけの使用による平面図形の作図である。例えば，与えられた線分ABを2等分する点Mを作図するには，AおよびBを中心として同じ半径で交わる円を描き，これら2円の交点をC，Dとして，線分CDと線分ABの交点をMとすればよい（図1）。次の作図も定規とコンパスだけで容易にできる。与えられた角AOBを2等分すること（図2），与えられた点Aを通り与えられた直線lに垂直な直線を引くこと（図3），与えられた正方形の2倍の面積をもつ正方形を作ること（図4）。そのほかの多種多様な作図もこの方法で可能である。しかしながら，指定された方法では作図が不可能なこともある。例えば，与えられた角を3等分することや，正七角形を作ることは定規とコンパスだけの使用では不可能であり（作図不能問題），また，与えられた角を2等分することや，中心の示されていない円の中心を求めることは定規の使用だけでは不可能である。上で述べたことからもわかるように，幾何学における作図は理論的性格のもので，図をできるだけ精確に描く方法を与えるものではなく，使用器具が完全な精度を有するとの仮定の下に，原理的に作図が可能であるかどうかを示すものである。
執筆者：中岡 稔

図1～図4

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

作図
さくず
construction

ある条件に適合する図形を描くこと。初等幾何学における作図とは，目盛りのない定規とコンパスを用いて図を描くこと，すなわち作図の公法，(1) 与えられた2点を結ぶ線分を引く，(2) 線分をいくらでも延長する，(3) 与えられた点を中心として与えられた長さを半径とする円を描く，に従って作図することを意味する。作図の公法に従って条件に合う図形を描くことを要求し，またはその可能性を問う問題を「作図題」といい，この図形を描くことを「作図題を解く」という。作図の公法に従って作図することが不可能である作図題を「作図不能問題」という。初等幾何学において，歴史的に著名な作図不能問題には，次の3つがある。 (1) 角の3等分問題　与えられた角を3等分すること。 (2) 立方体倍積問題またはデロスの問題　与えられた立方体の体積の2倍に等しい体積をもつ同型立方体をつくること。 (3) 円積問題　与えられた円と等積の正方形をつくること。以上を特に作図三大不能問題という。そのほか，正七角形，正九角形，正十一角形をつくること，円周に等しい長さの線分をつくることなど，多くの作図不能問題がある。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

作図【さくず】

幾何学で与えられた条件を満足する図形を描くこと。特に初等幾何学で定規とコンパスだけを用いて作図する問題を作図題という。→作図不能問題

出典　株式会社平凡社