等比数列（読み）トウヒスウレツ（英語表記）geometric progression

デジタル大辞泉

とうひ‐すうれつ【等比数列】

隣り合う二項間の比が一定の数列。一つの数に、一定の数を次々に掛けていってできる数列。幾何数列。

出典　小学館

精選版 日本国語大辞典

とうひ‐すうれつ【等比数列】

1. 〘 名詞 〙 隣り合う各項の比が常に一定であるような数列。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

等比数列 (とうひすうれつ)
geometric progression

例えば｛1，2，4，8，16，32，……｝や｛1，1/3，1/9，1/27，1/81，……｝のように，隣り合う2数の比が一定である数列を等比数列といい，その一定の比を公比という。上の二つの例では公比はそれぞれ2，1/3である。初項（第1項）がa，公比がrである等比数列の第n項a_nはa_n＝arⁿ⁻¹となる。また，この等比数列の初項から第n項までの和S_nは，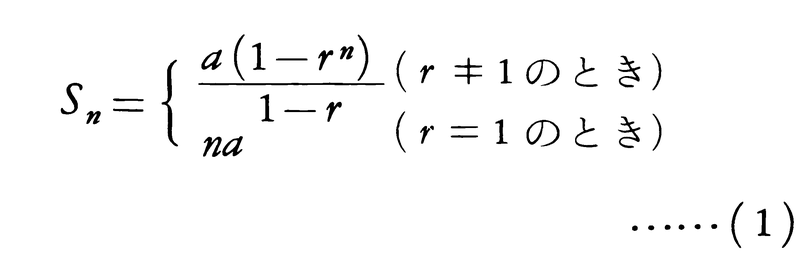

で与えられる。等比数列a，ar，ar²，……，arⁿ⁻¹，……をこの順に形式的に加号（＋）で結んだ式，

　a＋ar＋ar²＋……＋arⁿ⁻¹＋……　……（2）　

を等比級数geometric seriesというが，｜r｜≧1のときはこの無限級数は収束しないから，（2）は具体的な意味をもたない。｜r｜＜1ならばnが限りなく大きくなるときrⁿは0に限りなく近づくから，（1）のS_nの値は，S＝a/（1－r）に限りなく近づく。このSの値を｜r｜＜1のときの無限等比級数（2）の和という。一般に級数の第1項から第n項までの和S_nをその級数の部分和というが，等比級数の部分和の公式は（1）にほかならない。なお，等比数列そのもののことを等比級数，または幾何級数ということがある。
→級数
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

等比数列
とうひすうれつ

一つの数に、一定の数を次々に掛けていってできる数列。幾何数列ともいい、G. P.（geometric progression）と書くこともある。最初の数を初項、次々に掛ける一定数を公比という。初項をa、公比をrとするとき、その第n項a_nは、
　　a_n=ar^n-1
と表される。とくに、三つの数a₁,a₂,a₃が等比数列をなすとき、間の数a₂を等比中項という。等比中項は両端の数a₁、a₃の相乗平均（幾何平均）で表される。すなわち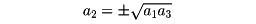

である（符号はどちらもありうる）。公比rが1の場合は、この等比数列はa,a,a,……となり、第n項までの和はnaである。r≠1のとき、初項a、公比r、項数nの等比数列の和をs_nとすれば、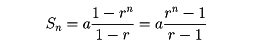

である。一般に利息計算で用いられる複利法は、元金a円、利率rとしたとき、一期間ごとに元利合計は
　　a,a(1+r),a(1+r)²,……
となっていく等比数列をなす。したがって、等比数列、およびその和の公式は、積立貯金、年金、年賦償還の計算などに広く利用される。

　等比数列の項が無限に続くものを無限等比数列という。この無限等比数列
　　a,ar,ar²,……
の項をプラスで結んでつくった式a+ar+ar²+……を等比級数という。この級数は、a≠0ならば|r|＜1のときにのみ収束し、その和は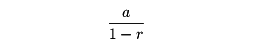

である。この級数は、もっとも基本的な級数として重要である。多くの級数の収束、発散を、無限等比級数との比較において論じることができる。

［竹之内脩］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

等比数列
とうひすうれつ
geometric progression (sequence)

幾何数列ともいう。1，3，9，27，…のように，数列 a₁ ，a₂ ，a₃ ，…，a_n ，…において，各数 a_n が，そのすぐ前の数 a_n-1 に一定数 r を掛けること (a_n＝a_n-1×r) によって得られるとき，この数列を等比数列という。各数 a_n をこの数列の項，その第1項を初項，r＝a_n/a_n-1 を公比という。公比が r の等比数列において，初項 a₁ から第 n 項 a_n＝a₁r^n-1 までの和 S_n は，r＝1 のとき S_n＝na₁ ，r≠1 のとき S_n＝a₁(1－rⁿ)/(1－r) の公式で求められる。公比 r の絶対値が1より小さいとき，かつそのときにのみ，n→∞ とした無限等比級数は収束する。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の等比数列の言及

【数列】より

…項の番号nに対応してa_nを定める規則が与えられれば，一つの数列が定義される。例えばa,d,rを定数とするとき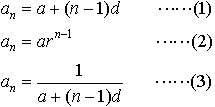，で定義される数列は，それぞれ等差数列，等比数列，調和数列と呼ばれる。また，a₁とa₂が与えられ，a_n＝1/2(a_n－1＋a_n－2)(n≧3)という規則が与えられれば，すべてのa_nが順次定まるから，一つの数列が定義される。…

※「等比数列」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」