改訂新版 世界大百科事典 「解の公式」の意味・わかりやすい解説
解の公式 (かいのこうしき)
formula for solutions
いくつかの型の方程式または連立方程式には,その解を与える公式があり,そのような公式を解の公式と呼ぶ。その中には,いくつかの型の微分方程式に関するものがある。また連立一次方程式についてのクラメールの公式も解の公式の一例である。その他の重要な場合は代数方程式の場合であるので,それについて述べる。この場合は根の公式とも呼ばれる。
(1)二次方程式aX2+bX+c=0(a≠0)の根は,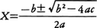
D=b2-4acを判別式discriminantという。D=0のときは2根が一致(重根)のときである。a,b,cがいずれも実数であるとき,この二次方程式が実根をもつのはD≧0のときであるので,判別式の正負によって根の実,虚が判別できる。a,b,cがいずれも有理数であるとき,根が有理数となるのはDが有理数の平方のときである。二次方程式がaX2+2bX+c=0の形のときは,根は,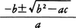 で与えられる。このときb2-ac(=1/4D)が上のDと同じ役をする。
で与えられる。このときb2-ac(=1/4D)が上のDと同じ役をする。
(2)三次方程式aX3+bX2+cX+d=0(a≠0)はX=Y-(b/3a)とおけば,Y3+3pY+q=0と変形する。ただし,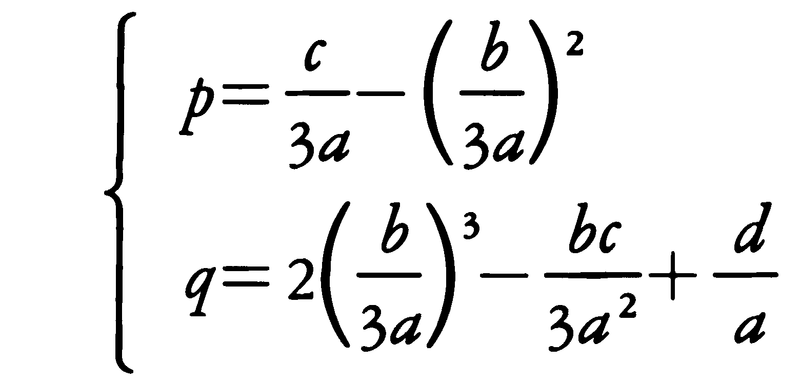
この新しい三次方程式の根は,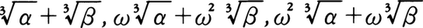 である。ただし,ωは1の虚立方根,
である。ただし,ωは1の虚立方根,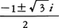 の一つ,α,βは,
の一つ,α,βは,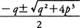 である(カルダノの解法)。-(q2+4p3)は(新,旧,両三次方程式の)判別式と呼ばれる。この判別式をDとすると,
である(カルダノの解法)。-(q2+4p3)は(新,旧,両三次方程式の)判別式と呼ばれる。この判別式をDとすると,
(Ⅰ) D=0ならば,重根がある。
(Ⅱ) a,b,c,dが実数のときには,
D>0 相異なる三つの実根をもつ。
D=0 一つ重根をもち,根はすべて
実根。
D<0 実根はただ一つ。
(3)三次方程式X3+3pX+q=0(p,q:実数,p≠0)の,三角関数を利用した公式がある。判別式D=-(q2+4p3)をとる。
(Ⅰ) D>0のときは,当然p<0であり,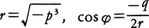
とおけば,3根は,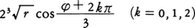
(Ⅱ) D<0,p<0のときは,θ, φを,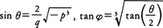
によって定めれば,実根は,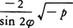
虚根は,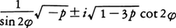
(Ⅲ) D<0,p>0のときは,θ,φを,
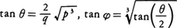
によって定めれば,実根は,
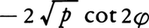
虚根は,
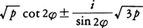
(Ⅳ) D=0のとき,単根は,
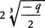
重根は,
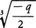
(4)四次方程式X4+aX3+bX2+cX+d=0(a≠0)については,X=Y-(b/4a)とおけば,
Y4+pY2+qY+r=0 ……(1)
の形に変形できる。この方程式に対して,
T3-pT2-4rT+(4pr-q2)=0 ……(2)
の一つの根tをとれば,(1)の根は,次の二つの二次方程式の根として得られる(フェラリの解法)。
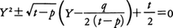
また,
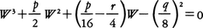 ……(3)
……(3)
の3根をu2,v2,w2とすると,(1)の根は,
u+v+w,u-v-w,
-u+v-w,-u-v-w
である(オイラーの解法)。
(5)五次以上については(2)(4)のような公式はない。特別な形をしているためにやさしく解けるものはある。
例 a0Xn+a1Xn⁻1+……+an=0(a0≠0)
において,ai=an-1(i=0,1,2,……,n)であるとき,これを相反方程式という。
(Ⅰ) nが奇数ならば-1が一つの根である。
(Ⅱ) nが偶数ならばt=x+x⁻1とおいてtについてのn/2次方程式に帰着できる。なお,Xn-1=0の根は,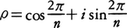 とおけば,ρ,ρ2,……,ρn⁻1,ρn=1であるが,この方程式を代数的に解くことは可能ではあるが,一般にはたいへんめんどうである。やさしい例をあげると,
とおけば,ρ,ρ2,……,ρn⁻1,ρn=1であるが,この方程式を代数的に解くことは可能ではあるが,一般にはたいへんめんどうである。やさしい例をあげると,
執筆者:永田 雅宜
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

