判別式（読み）ハンベツシキ（その他表記）discriminant

デジタル大辞泉

はんべつ‐しき【判別式】

二次方程式ax²＋bx＋c＝0について、その根の種類を判別するためのD＝b²－4acという式。Dが正ならば二つの実根、0ならば重根、負ならば二つの虚根をもつ。

出典　小学館

精選版 日本国語大辞典

はんべつ‐しき【判別式】

1. 〘 名詞 〙 二次方程式の根の種類を判定するための式。二次方程式 ax₂+bx+c=0（a0） に対し、b₂-4ac をその判別式といい、記号Ｄで表わす。D＞0 のとき異なる二実根、D=0 のとき重根、D＜0 のとき虚根となる。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

判別式 (はんべつしき)
discriminant

n次代数方程式f（X）＝a₀Xⁿ＋a₁Xⁿ⁻¹＋a₂Xⁿ⁻²＋……＋a_n＝0の根をα₁，α₂，……，α_nとするとき，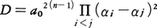

を方程式f（X）＝0の判別式という。根と係数の関係を使って，判別式Dは方程式の係数a₀，a₁，……，a_nの多項式として表すことができる。例えば二次方程式aX²＋bX＋c＝0の判別式Dは，

　D＝a²（α₁－α₂）²＝a²｛（α₁＋α₂）²－　　4α₁α₂｝＝b²－4ac

である。また三次方程式X³＋pX＋q＝0の判別式はD＝－4p³－27q²である。判別式の定義から明らかなように，方程式f（X）＝0が重根をもつための必要十分条件はD＝0が成立することである。例えば二次方程式aX²＋bX＋c＝0が重根をもつための必要十分条件はb²－4ac＝0であり，三次方程式X³＋pX＋q＝0が重根をもつための必要十分条件は4p³＋27q²＝0である。

　二次方程式aX²＋bX＋c＝0の係数a，b，cがすべて実数のときは，判別式D≧0であることが実根をもつための必要十分条件であり，D＜0が2虚根をもつための必要十分条件である。同様にして実数を係数とする三次方程式に対しては，D＞0であれば方程式は相異なる3実根をもち，D＝0であれば根はすべて実根であり，そのうちの少なくとも二つは等しく，D＜0であれば方程式は1実根と2虚根をもつ。またこの逆も成立する。

　なお，整数論で使われる判別式は上で定義したものとは別のものである。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

判別式
はんべつしき

n次方程式
　　f(x)=a₀xⁿ+a₁x^n-1+……+a_n=0
の解をα₁,α₂,……,α_nとするとき
　　D=a₀^2(n-1)(α₁-α₂)²
　　　 ×(α₁-α₃)²……
　　　 (α₁-α_n)²
　　　 ×(α₂-α₃)²……
　　　 (α₂-α_n)²
　　　 ×………………
　　　 ×(α_n-1-α_n)²
をf(x)=0の判別式という。

　n=2でf(x)=ax²+bx+c=0のときは、二つの解をα、βとすると
　　D=a²(α-β)²=b²-4ac
であり、f(x)=0の解は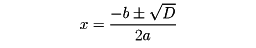

と表される。

　n=3でf(x)=ax³+bx²+cx+d=0のときには、三つの解をα、β、γとして
　　D=a⁴(α-β)²(α-γ)²(β-γ)²
　　 =b²c²+18abcd-4ac³-4b³d
　　　-27a²d²
とくにf(x)=x³+cx+dのときは
　　D=-4c³-27d²
でありf(x)=0の解は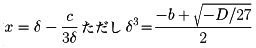

と表される。δのとり方は、三乗して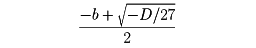

となる数を一つとり、それをδ₀として、δ₀ω,δ₀ω²（ωは1の立方根）をつくればよいので、三つのxの値が定まる。

　有理数を係数とする既約方程式f(x)=0の解をαとし、有理数体Qにαを付加した体をQ(α)とする。f(x)=0の判別式は整数であり、その値はQ(α)の整数論的な構造に重要な意味をもっている。

［寺田文行］

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

判別式【はんべつしき】

n次方程式a(/0)x(n/)＋a₁x(n/)(-/)¹＋…＋a(/n)＝０のn個の根x₁，x₂，…，x(/n)の差の２乗を掛け合わせた式を初めの方程式の判別式という。この方程式が重根をもつための必要十分条件はD＝０となることである。Dはa(/0)，a₁，…，a(/n)の多項式になり，二次方程式ax²＋bx＋c＝０ではD＝b²−４ac，三次方程式x³＋px＋q＝０では，D＝−４p³−27q²。

出典　株式会社平凡社

世界大百科事典（旧版）内の判別式の言及

【解の公式】より

…この場合は根の公式とも呼ばれる。(a)二次方程式aX²＋bX＋c＝0(a≠0)の根は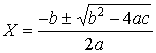，D＝b²－4acを判別式discriminantという。D＝0のときは2根が一致(重根)のときである。…

【二次方程式】より

…a,b,cが整数の場合に，n/m(既約分数)が根となりうるのは，mがaの約数であり，nがcの約数(負の約数も含める)である場合に限られる。　D＝b²－4acを上の二次方程式の判別式discriminantという。これを用いると二次方程式の2根は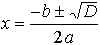，で与えられる。…

【解の公式】より

…この場合は根の公式とも呼ばれる。(a)二次方程式aX²＋bX＋c＝0(a≠0)の根は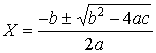，D＝b²－4acを判別式discriminantという。D＝0のときは2根が一致(重根)のときである。…

【二次方程式】より

…a,b,cが整数の場合に，n/m(既約分数)が根となりうるのは，mがaの約数であり，nがcの約数(負の約数も含める)である場合に限られる。　D＝b²－4acを上の二次方程式の判別式discriminantという。これを用いると二次方程式の2根は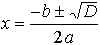，で与えられる。…

※「判別式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」