陰関数（読み）いんかんすう（英語表記）implicit function

精選版 日本国語大辞典

いん‐かんすう ‥クヮンスウ【陰関数・陰函カン数】

〘名〙 変数ｘ、ｙの関係式 F(x, y)=0 （たとえば x²+y²-l=0）が与えられれば、ｘの各値に、これをみたすｙの値を対応させることによって、一つの関数 y=f(x) が定まる。これを F(x, y)=0 によって定まるという。関数 y=f(x) が関係式 F(x, y)=0 の陰(かげ)に隠れているところからいう。⇔陽関数

出典　精選版 日本国語大辞典

デジタル大辞泉

いん‐かんすう〔‐クワンスウ〕【陰関数】

二つの変数xとyの関係がf（x,y）＝0の形で表され、yの値が直接xの値で示されていない関数。例えばx²＋y²－1＝0やx²＋2xy＋y²＝1など。⇔陽関数。

出典　小学館

日本大百科全書(ニッポニカ)

陰関数
いんかんすう
implicit function

ある方程式、たとえばx²＋y²＝1が与えられると、xの値を一つ定めれば、これから対応するyの値が求められ、yはxの関数として定まる。このようにして定められる関数を陰関数という。一般に二つの変数x、yに対して、2変数x、yの関数をゼロと置いた方程式f(x,y)＝0において、xの値を決めたとき、yの値をf(x,y)＝0を満たすようにただ一つ決めることができれば、yはxの関数となる。これは通常狭い範囲に考察を限らないといえない。すなわちx²＋y²＝1では、xは－1≦x≦1を満たす範囲になければならず、またそのときも、x²＋y²＝1からは一般にyの値が二つ出てくるので、それが一つに定まるように、ある点の近くで考えることにしなければならない。

　前記のような事情から（関数が具体的な形で与えられた場合は別として）、一般に陰関数を考察するためには、次の定理が基礎とされる。

［竹之内脩］

陰関数定理

f(x,y)はx、y2変数の連続関数で、そのyに関する偏導関数f_y(x,y)が存在して連続であるとする。そのとき、
　　f(x₀,y₀)＝0,　f_y(x₀,y₀)≠0
を満足する点（x₀,y₀）の近傍において、yはxの関数として表すことができる。すなわち、x₀の近傍で定義された連続関数g(x)があって、
　　g(x₀)＝y₀，f(x,g(x))＝0
が成立する。

［竹之内脩］

[参照項目] | 関数

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

陰関数
いんかんすう
implicit function

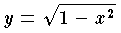陰伏関数ともいう。本来の関数ではないが，2つの変数 x，y が f(x，y)＝0 という関係で縛られているとき，変数 x に対して，ある条件下ではこうして拘束される y がただ1つ定まるので，y を x の関数と考えることができるようになる。たとえば，x²＋y²－1＝0 についてなら，y＞0 については という関数が得られる。このように，関数を陰に隠しているように含んでいる関係という意味で，習慣的に陰関数という用語が用いられている。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

陰関数【いんかんすう】

変数x，yの間の関係式F（x，y）＝０によってxの関数yが定義されるとき，yをxの陰関数という。陽関数の対。
→関連項目関数

出典　株式会社平凡社

世界大百科事典（旧版）内の陰関数の言及

【関数】より

…例えばm＝2のとき，実数tの関数の組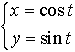，は，定義域が実数の全体，値域が二次元空間，すなわち平面の中の集合(この場合は単位円周：x²＋y²＝1)である関数を与える。
［陰関数，陽関数］
　2変数の関数F(x,y)が与えられていて，F(x,y)＝0という関係によってyがxの関数として定まるとき，それを陰関数という。これに対し，上記のようにy＝f(x)の形に表される関数を陽関数という。…

※「陰関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」