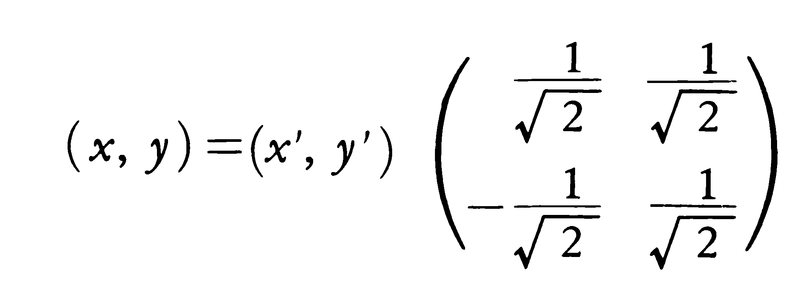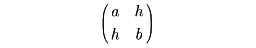主軸変換 (しゅじくへんかん)
transformation of principal axis
ax2+bxy+cy2+dx+ey+f=0 (b2-4ac≠0)
で与えられる二次曲線αを考えよう。αは点((2cd-be)/(b2-4ac),(-bd+2ae)/(b2-4ac))に関して対称で,原点をこの点に移すと,αは,
ax2+bxy+cy2+f′=0
で与えられる。αが直線lに関して対称であるとき,lをαの主軸という。αには互いに直交する二つの主軸が存在し,それらを直交軸に選ぶことによってαは,
a′x2+c′y2+f″=0
と簡単な形で与えられる。このように変形することを主軸変換するという。
例えばx2+4xy+y2-1=0で与えられる二次曲線は,直線y=x,y=-xについて対称で,これを直交軸にとると,すなわち,
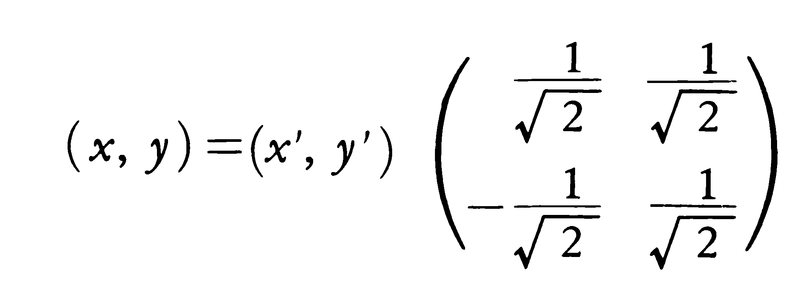
と変換すれば-x′2+3y′2-1=0となる。このような変換は一般に次の式で与えられる二次超曲面の場合にも考えられる。

執筆者:斎藤 裕
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
主軸変換
しゅじくへんかん
与えられた二次式
f(x, y)=ax2+2hxy+by2+c
に対して、座標系を適当な角度だけ回転して新しい座標系をつくれば、
f(X, Y)=lX2+mY2+n
のようにxyの項がなくなるようにできる。このように二次式の変数の積の項をなくすような回転移動を主軸変換(主軸への変換という意味)という。二次式で表される曲線、すなわち二次曲線が、ある直線に関して対称になっているとき、この直線を主軸という。楕円(だえん)と双曲線は直交する2本の主軸をもち、放物線は1本の主軸をもつ。したがって二次式の主軸変換をすることは、この二次曲線の主軸に平行な直線を座標系にとることにほかならない。また対称行列を対角化すること、すなわち対称行列Sに対し、適当に直交行列Uを選び、U-1SUを対角行列とすることを主軸変換ということもある。平面を自分自身に写す線形写像fは、平面に一つの正規直交基底を決めるたびに行列で表現できる。それが対称行列のときは、新たに適当な正規直交基底を選ぶと、これに関してfを行列により表現したものが対角形になることが知られている。このとき、旧正規直交基底を新正規直交基底に写すような直交変換をfの主軸変換という。
以上の2種類の主軸変換は見かけ上異なるが、二次式ax2+2hxy+by2を対称行列
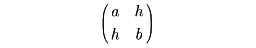
に対応させて考えてみれば、内容的に同一のものであることがわかる。なお、線形写像の立場からいうと、先述の新正規直交基底はfの固有ベクトルになっている。
[高木亮一]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
主軸変換
しゅじくへんかん
transformation of principal axis
2次形式を対角化する変換のこと。たとえば Σijaijxixj という2次形式を x'i=Σijbijxj という線形変換によって,2次形式の標準形 Σa'i(x'i)2 に変形する交換が主軸変換である。理論上では2次形式を表わす対称行列の固有ベクトルのつくる正規直交系を座標軸とする変換である。物理学においても主軸変換の応用は広く,回転している物体の慣性モーメントの問題などに使われる。量子力学では一般に物理量は行列で表わされるから,ユニタリ変換によって対角行列に変換して固有値を求める。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by