関連語
改訂新版 世界大百科事典 「部分分数」の意味・わかりやすい解説
部分分数 (ぶぶんぶんすう)
partial fraction
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「部分分数」の意味・わかりやすい解説
部分分数
ぶぶんぶんすう
partial fraction
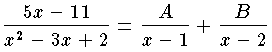 を,A ,B を定数として
を,A ,B を定数として 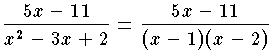 の形に書直すことを試みれば,分母を払って係数を比較して A=6,B=-1 であることがわかる。微分や積分は加法的な演算なので,分数式の微積分には部分分数分解が有効になる。
の形に書直すことを試みれば,分母を払って係数を比較して A=6,B=-1 であることがわかる。微分や積分は加法的な演算なので,分数式の微積分には部分分数分解が有効になる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

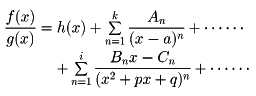
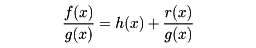


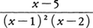 は,次のように変形される。
は,次のように変形される。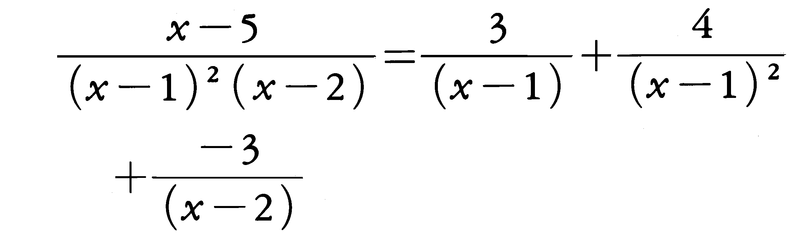
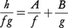 で,deg A<deg f,deg B<deg gを満たす多項式A,Bが定まる。(2)nが2以上の自然数で,deg h<degfnならば,
で,deg A<deg f,deg B<deg gを満たす多項式A,Bが定まる。(2)nが2以上の自然数で,deg h<degfnならば,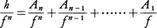 で,deg Ai<deg f(1≦i≦n)である多項式Aiが定まる。(1),(2)のA,B,Aiは
で,deg Ai<deg f(1≦i≦n)である多項式Aiが定まる。(1),(2)のA,B,Aiは