未定係数法（読み）みていけいすうほう（その他表記）method of indeterminate coefficients

改訂新版　世界大百科事典

未定係数法 (みていけいすうほう)
method of indeterminate coefficients

有理式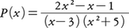，を部分分数に分解することを考えよう。それには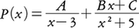，と展開できたとして，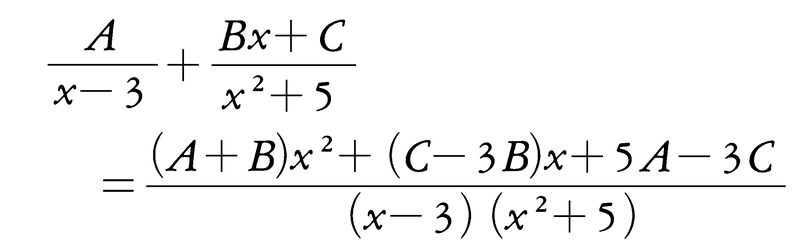

であるから，係数を比較して，

　A＋B＝2，C－3B＝－1，

　5A－3C＝－1

であればよい。この一次方程式を解くと，A＝1，B＝1，C＝2であるから部分分数展開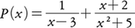，を得る。このように求めたい係数を未知数にしておいて，それらが満たす条件からその係数を決める方法を未定係数法という。次にこの方法の応用例をいくつか示そう。

因数分解

多項式，

　f（x，y）＝2x²＋3xy－2y²＋5x＋5y＋3

を因数分解することを考えよう。それには，

　f（x，y）＝（ax＋by＋c）（dx＋ey＋f）

と分解できたとして，係数a，b，c，d，e，fを決めればよい。ここで，これらの係数は整数としてよい。x²の係数を比較して，ad＝2であるから，a＝1，d＝2としてよい。xyとy²の係数を比較してbe＝－2，e＋2b＝3を得，これからb＝2，e＝－1と定まる。次にx，yの係数および定数項を比較して，c＝1，f＝3が決まり，因数分解，

　f（x，y）＝（x＋2y＋1）（2x－y＋3）

が求まる。因数分解は簡単な場合はこの方法でできるが，一般にはむずかしい。

微分方程式

微分方程式，

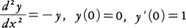を考えよう。解がy＝a₀＋a₁x＋a₂x²＋……の形の展開をもったとすると，

　n（n－1）a_n＝－a_n-2　（n≧2，a₀＝1，a₁＝1）　

でなければならない。これから，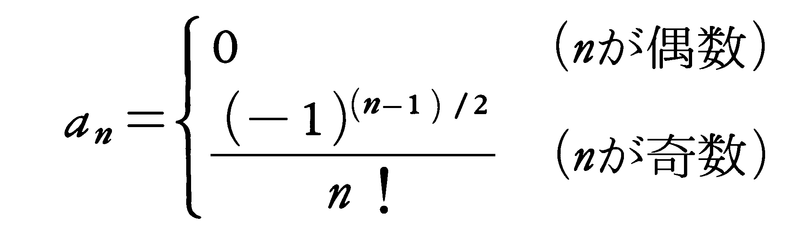

が得られるが，級数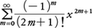，は収束して，微分方程式の解sin xを与える。

ラグランジュの未定係数法

二つの2変数関数f（x，y），g（x，y）に対して，g（x，y）＝0という条件の下でf（x，y）の極値を求めることを考える。ここでf，gについての微分可能性の条件と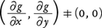，を仮定する。このときfが（x₀，y₀）で極値をとるとすると，あるλ₀があって，（x₀，y₀，λ₀）はx，y，λの方程式，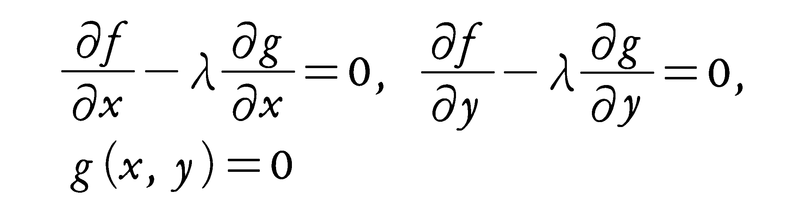

の解になっているから，これを解けばよい。このようにして（x₀，y₀）を求める方法をラグランジュの未定係数法という。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

未定係数法
みていけいすうほう

与えられた既知の式または条件から新しい式を導くとき、求めるべき式に現れる係数を未知数として設定し、種々の数学的原理を用いて、未知の係数を決定する方法を未定係数法という。以下三つの応用例を示す。

（1）2x³-x²+3x+1をx²-2x+3で割ったときの商と余りを求める。商と余りはいずれも一次式であるから、それぞれをax+b,cx+dと置くと、次の等式が得られる。

　　2x³-x²+3x+1
　　　=(x²-2x+3)(ax+b)+(cx+d)
これは恒等式であるから、左右の同類項の係数は等しい。

　　a=2, 2a-b=1, 3a-2b+c=3,　3b+d=1
この連立方程式を解いて、
　　a=2, b=3, c=3, d=-8
を得る。したがって、商は2x+3で、余りは3x-8である。

（2）xの三次の整式があって、xが-1,0,1,2の値をとるとき、この式の値は、それぞれ、-1,3,5,11となる。この整式を求める。求める整式をf(x)=ax³+bx²+cx+dと置くと、
　　f(-1)=-a+b-c+d=-1,
　　f(0)=d=3,
　　f(1)=a+b+c+d=5,
　　f(2)=8a+4b+2c+d=11
が得られる。これらの方程式から
　　a=1,b=-1,c=2,d=3
を得る。求める式はx³-x²+2x+3である。

（3）次の恒等式が成立するように定数a,b,cの値を求める。

　　a(x-1)(x-2)+b(x-2)(x-3)
　　　+c(x-3)(x-1)=4x²-13x+7
恒等式であるから、xに任意の数を代入しても、両辺の式の値は等しい。そこでxにそれぞれ1,2,3を代入すると、それぞれ
　　2b=-2,-c=-3,2a=4
が成り立つ。これからa=2,b=-1,c=3が得られる。

［竹内芳男］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

未定係数法
みていけいすうほう
method of undetermined coefficients

ある条件を満たす未知関数 f を求めるのに，たとえば，f が多項式であることがわかっていたりすると，f(x)＝c₀＋c₁x＋c₂x²＋…＋c_nxⁿ として，最初の条件を c_k についての条件に直し，それから c_k を求めることによって f を決定する方法をいう。

出典　ブリタニカ国際大百科事典 小項目事典