コンピュータにおける数値の表現（読み）こんぴゅーたにおけるすうちのひょうげん

日本大百科全書(ニッポニカ)

コンピュータにおける数値の表現
こんぴゅーたにおけるすうちのひょうげん

〔二進記数法〕
　コンピュータで数値を表現するには、普通、二進記数法を用いる。二進記数法とは、0と1の2種類の数だけを用いて数値を表現する方法である。1語が4ビットであるとすると、0000から1111までの数値が表現できるので、十進記数法の0から15までの数値が表現できる。

　　（二進法）　　（十進法）
　　0000　　　　　　0
　　0001　　　　　　1
　　0010　　　　　　2
　　0011　　　　　　3
　　0100　　　　　　4
　　0101　　　　　　5
　　0110　　　　　　6
　　0111　　　　　　7
　　1000　　　　　　8
　　1001　　　　　　9
　　1010　　　　　10
　　1011　　　　　11
　　1100　　　　　12
　　1101　　　　　13
　　1110　　　　　14
　　1111　　　　　15
　つまり1語がnビットであるとし、1語で表現できる数値をaとすると、
　　0≦a≦2ⁿ－1
となる。

〔負の数の表し方〕
　ところで、このままでは負の数を表すことができない。そこで、aを2ⁿで割ったときに絶対値が最小になる余りをa′とする。

　たとえばn＝4（1語が4ビット）の場合、aが10のときのa′はどうなるかみてみることにしよう。10を2⁴すなわち16で割ると、商は0、余りは10になる。ここで、商を1とすると、余りは－6になる。ついで、商を－1、－2、－3、……としてみると、余りは26、42、58、……としだいに大きくなり、商を2、3、4、……としてみると、余りは－22、－38、－54、……と、その絶対値はしだいに大きくなる。すなわち、10を16で割ったときに絶対値が最小になる余りは－6であることがわかる。

　このようにして、n＝4のときのaとa′の関係を調べてみると、次のようになる。

　 a′｜ a　｜aのビット表現
　―――――――――――――
　　7｜　7｜0111
　　6｜　6｜0110
　　5｜　5｜0101
　　4｜　4｜0100
　　3｜　3｜0011
　　2｜　2｜0010
　　1｜　1｜0001
　　0｜　0｜0000
　－1｜15｜1111
　－2｜14｜1110
　－3｜13｜1101
　－4｜12｜1100
　－5｜11｜1011
　－6｜10｜1010
　－7｜　9｜1001
　－8｜　8｜1000
　―――――――――――――
　つまり、一般には次のようになる。

　　a≡a′(mod2ⁿ)
　　－2^n－1＝－2ⁿ/2≦a′＜2ⁿ/2＝2^n－1
　すなわち、a＜2^n－1のとき（上の例ではaが8よりも小さいとき）はa′＝aであり、a≧2^n－1のとき（上の例ではaが8以上のとき）はa′＝a－2ⁿ（上の例ではa′＝a－16）である。ところで、
　　a－2ⁿ＝a－(2^n－1＋2^n－1)
　　　 　　　＝(a－2^n－1)－2^n－1
であるから、1語の最左端のビットに－2^n－1という位取りを与え、残りのビットには通常の二進位取りを与えたと考えることもできる。

　たとえば1語を4ビットとすると、
　　0000　は　0＋0＋0＋0＝0
　　0001　は　0＋0＋0＋2⁰＝1
　　0010　は　0＋0＋2¹＋0＝2
　　　…　…　　　　…　　　　…
　　　…　…　　　　…　　　　…
　　0111　は　0＋2²＋2¹＋2⁰＝7
　　1000　は　－2³＋0＋0＋0＝－8
　　1001　は　－2³＋0＋0＋2⁰＝－7
　　1010　は　－2³＋0＋2¹＋0＝－6
　　　…　…　　　　　…　　　　　…
　　　…　…　　　　　…　　　　　…
　　1111　は　－2³＋2²＋2¹＋2⁰＝－1
というぐあいである。

〔補数方式〕
　このように表現すると、負数（－x）の表現はa－2ⁿである。したがって
　　(－x)＝a－2ⁿ
したがって
　　2ⁿ＝a＋x
である。つまり、負数の表現は、1語で表される数をaとしたときの正数の表現と、2ⁿに関して互いに補数になっている。したがって、この表現方式を補数方式という。補数方式で表現しても、加減算は通常の方法で行うことができる。

　　　0011…… 3　　0011…… 3
　　＋0010…… 2　＋1011……－5
　　――――――――――――
　　　0101…… 5　　1110……－2
　　　0100…… 4　　1100……－4
　　－0110…… 6　－1101……－3
　　――――――――――――
　　　1110……－2　 1111……－1
　ところで、減算a′－b′を考えると、b′の補数を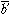と表すなら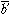（はb′を表現しているビットの0と1を逆にしたものに1を加えたものになっていることに注意しよう）、補数方式では
　　a′－ b′＝a′＋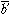
となるので、減算は加算によって行うことができる。

　　　0100…… 4　　0100…… 4
　　－0110…… 6　＋1010…… 6
　　――――――――――――
　　　1110……－2　 1110……－2

〔小数点の表示〕
　普通、コンピュータでは最左端のビットの右に小数点を想定した固定小数点表示が用いられている。

　すると、1語で表される数をaとすると、実際に表現している数値は、a×2^－(n－1)となるので、補数方式をとったとすると、
　　－1＝－2^n－1×2^－(n－1)≦a′＜2^n－1×2^－(n－1)＝1
の範囲の数を2^－(n－1)刻みで表現したものになる。

　このとき
　　a＋x＝2ⁿ×2^－(n－1)＝2
となるので、補数方式を「2の補数」とよぶことが多い。

〔浮動小数点表示〕
　コンピュータでは、小数点以下の数をもつ値Yは、普通、
　　Y＝m×B^e
となる一対の値（m, e）で表現する。これを浮動小数点表示という。Bを底、mを仮数、eを指数とよぶ。仮数としては正の場合には1/B≦m＜1、負の場合には－1≦m＜1/Bとなるような表現を選ぶ。これを正規形という。一般に、底Bとしては2または16を用いている。

［土居範久］

[参照項目] | コンピュータ

出典　小学館　日本大百科全書(ニッポニカ)