関連語
精選版 日本国語大辞典 「ドモルガンの法則」の意味・読み・例文・類語
ド‐モルガン の 法則(ほうそく)
ブリタニカ国際大百科事典 小項目事典 「ドモルガンの法則」の意味・わかりやすい解説
ド・モルガンの法則
ド・モルガンのほうそく
de Morgan laws
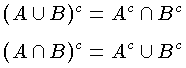 これをド・モルガンの法則という。この法則は集合の演算にとって基本的なものの一つである。
これをド・モルガンの法則という。この法則は集合の演算にとって基本的なものの一つである。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
法則の辞典 「ドモルガンの法則」の解説
ド=モルガンの法則【de Morgan's rule,de Morgan's law】
改訂新版 世界大百科事典 「ドモルガンの法則」の意味・わかりやすい解説
ド・モルガンの法則 (ドモルガンのほうそく)
→集合
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
世界大百科事典(旧版)内のドモルガンの法則の言及
【集合】より
…あるいは,集合Sで番号づけられた部分集合Aσ(σ∈S)が与えられたとき,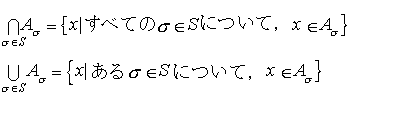 A,B,Cが集合Mの部分集合であるとき,次の等式が成り立つ。(1)交換法則 A∩B=B∩A A∪B=B∪A(2)結合法則 (A∩B)∩C=A∩(B∩C)=A∩B∩C (A∪B)∪C=A∪(B∪C)=A∪B∪C(3)分配法則 A∩(B∪C)=(A∩B)∪(A∩C) A∪(B∩C)=(A∪B)∩(A∪C)(4)吸収法則 A∪(A∩B)=A A∩(A∪B)=A(5)ド・モルガンの法則 (A∩B)c=Ac∪Bc (A∪B)c=Ac∩Bcもっと一般に,Sで番号づけられた部分集合Nσについて,
A,B,Cが集合Mの部分集合であるとき,次の等式が成り立つ。(1)交換法則 A∩B=B∩A A∪B=B∪A(2)結合法則 (A∩B)∩C=A∩(B∩C)=A∩B∩C (A∪B)∪C=A∪(B∪C)=A∪B∪C(3)分配法則 A∩(B∪C)=(A∩B)∪(A∩C) A∪(B∩C)=(A∪B)∩(A∪C)(4)吸収法則 A∪(A∩B)=A A∩(A∪B)=A(5)ド・モルガンの法則 (A∩B)c=Ac∪Bc (A∪B)c=Ac∩Bcもっと一般に,Sで番号づけられた部分集合Nσについて,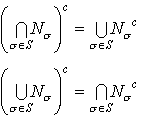 ド・モルガンの法則は,一つの集合の部分集合についての⊆,⊇,=,∩,∪を使った関係式は,各部分集合をその補集合に置きかえ,=はそのままにして,⊆と⊇とを取りかえ,∩と∪とを取りかえたものと同値であることを示している。これを集合算の双対性という。…
ド・モルガンの法則は,一つの集合の部分集合についての⊆,⊇,=,∩,∪を使った関係式は,各部分集合をその補集合に置きかえ,=はそのままにして,⊆と⊇とを取りかえ,∩と∪とを取りかえたものと同値であることを示している。これを集合算の双対性という。…
※「ドモルガンの法則」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

