フェルミ分布
フェルミブンプ
Fermi distribution
フェルミ統計にもとづく状態の数W{nj}から,系の全粒子数一定,
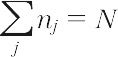
全エネルギー一定,
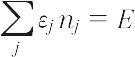
の条件のもとに平衡分布{nj*}が次のように求められる([別用語参照]量子統計力学).
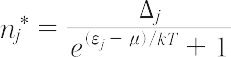
ただし,kはボルツマン定数,Tは絶対温度,Δj はエネルギー準位 εj にある状態の数,μは粒子数一定という条件から決まるパラメーターで,化学ポテンシャルに等しい.この分布をフェルミ分布またはフェルミ-ディラック分布という.μが正でkTに比べて十分大きい値をとるとき,フェルミ気体としての特徴がもっともよく現れる.フェルミ分布関数
f(ε) = {e(ε - μ)/kT + 1}-1
は,図のような形で示される.
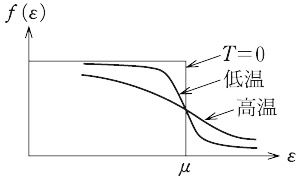
フェルミ分布の場合,化学ポテンシャルμをフェルミ準位またはフェルミ-ポテンシャルということが多い.絶対温度T = 0 K の極限では,領域ε < μでf(ε) = 1,ε > μでf(ε) = 0となる.これはフェルミ統計では,粒子は一つの状態に1個しか入れないので,エネルギーの低い準位から順に入り,ε = μのエネルギー準位までで全部の粒子N個がおさまってしまうことを示す.状態密度g(ε)を用いて,
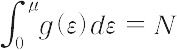
から,
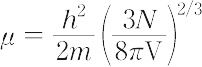
と決められる(hはプランク定数,mは粒子の質量,Vは系の体積).
T0 = μ/k
で定義される温度をフェルミ温度あるいは縮退温度という.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
Sponserd by 
フェルミ分布
フェルミぶんぷ
Fermi distribution
温度が T のとき,フェルミ統計に従う粒子がエネルギー ε の状態にある確率,またはこの状態にある粒子の平均数は次式で与えられる。
f(ε)=1/{ exp [(ε-ζ)/kT]+1}
この式で表わされる分布をフェルミ分布といい,ζ をフェルミエネルギーという。 k はボルツマン定数。温度が低いとき,この分布では,エネルギーが ζ 以下の状態は粒子によって完全に占められ,ζ 以上の状態には粒子がほとんどない。すなわち,ζ は粒子がもつ最大のエネルギーであって,粒子の化学ポテンシャルに等しく,固体電子論で重要な役割を演じる。また十分に温度が高ければ,フェルミ分布は古典的な気体分子運動論におけるマクスウェル=ボルツマン分布に等しい。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
法則の辞典
「フェルミ分布」の解説
フェルミ分布【Fermi distribution】
「フェルミ‐ディラック分布関数」のページをご覧ください。
出典 朝倉書店法則の辞典について 情報
Sponserd by 
世界大百科事典(旧版)内のフェルミ分布の言及
【フェルミ=ディラック分布】より
…量子状態jを占めている粒子の数njを観測すれば,1回の観測では0または1であるが,粒子集団が絶対温度Tの熱平衡にあれば,粒子数の平均値は,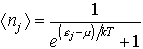 で与えられる。これをフェルミ=ディラック分布,または単にフェルミ分布Fermi distributionという。ここにkはボルツマン定数,μは
で与えられる。これをフェルミ=ディラック分布,または単にフェルミ分布Fermi distributionという。ここにkはボルツマン定数,μは[化学ポテンシャル]で,後者は〈n1〉+〈n2〉+……が粒子の総数に等しくなるという条件で決まる。…
※「フェルミ分布」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
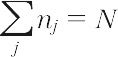
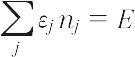
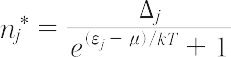

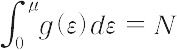
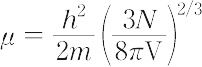


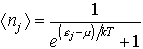 で与えられる。これをフェルミ=ディラック分布,または単にフェルミ分布Fermi distributionという。ここにkはボルツマン定数,μは
で与えられる。これをフェルミ=ディラック分布,または単にフェルミ分布Fermi distributionという。ここにkはボルツマン定数,μは