マクスウェル=ボルツマン分布 (マクスウェルボルツマンぶんぷ)
Maxwell-Boltzmann's distribution
古典力学に従う理想気体において,熱平衡状態での分子の各状態の確率分布をいう。N個の粒子からなる系の熱平衡状態において,速度v=(vx,vy,vz)の各成分vα(α=x,y,z)の値が,vαとvα+dvαの間にあるような粒子の数は,dvαがすべて小さいときn(v)dvxdvydvzで与えられる。このn(v)を速度分布関数という。古典統計力学(ボルツマン統計)では,系が絶対温度Tの熱平衡にあるとき,速度分布関数は,
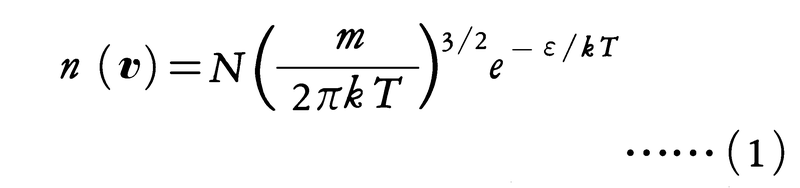
で与えられる。ただし,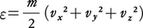 は粒子の運動エネルギーであり,mは粒子の質量,kはボルツマン定数である。(1)の速度分布をマクスウェルの速度分布則という。これは最初J.C.マクスウェルによって与えられたものであり,のち,L.ボルツマンによって一般化された。量子統計力学では(1)に対応するものは,粒子間の相互作用を無視したときのフェルミ粒子系のフェルミ=ディラック分布やボース粒子系のボース=アインシュタイン分布である。これらの分布関数はいずれも古典極限(2πmkT/(N/V)2/3≫h2)ではe⁻ε/kt・eμ/ktとなり,これはマクスウェル=ボルツマン分布にほかならないことがわかる。ここで,hはプランク定数,Vは粒子を入れた容器の体積,μは化学ポテンシャルである。またフェルミ=ディラック分布やボース=アインシュタイン分布は1粒子状態への分布で,定義からすると,速度分布関数に(h3/m3V)を乗じたものに対応していることに注意する。また,
は粒子の運動エネルギーであり,mは粒子の質量,kはボルツマン定数である。(1)の速度分布をマクスウェルの速度分布則という。これは最初J.C.マクスウェルによって与えられたものであり,のち,L.ボルツマンによって一般化された。量子統計力学では(1)に対応するものは,粒子間の相互作用を無視したときのフェルミ粒子系のフェルミ=ディラック分布やボース粒子系のボース=アインシュタイン分布である。これらの分布関数はいずれも古典極限(2πmkT/(N/V)2/3≫h2)ではe⁻ε/kt・eμ/ktとなり,これはマクスウェル=ボルツマン分布にほかならないことがわかる。ここで,hはプランク定数,Vは粒子を入れた容器の体積,μは化学ポテンシャルである。またフェルミ=ディラック分布やボース=アインシュタイン分布は1粒子状態への分布で,定義からすると,速度分布関数に(h3/m3V)を乗じたものに対応していることに注意する。また,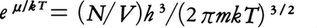 に注意すると,古典極限におけるマクスウェル=ボルツマン分布への移行が明らかになろう。
に注意すると,古典極限におけるマクスウェル=ボルツマン分布への移行が明らかになろう。
速度分布(1)から直ちに得られる結論の一つは運動エネルギーの等分配則である。温度Tの熱平衡状態では,質量の大きな粒子も小さな粒子も,また粒子間相互作用のいかんによらず,各粒子の運動エネルギーの平均値は等しく(3/2)kTである。このようなエネルギー等分配の法則は量子統計では成り立たない。
執筆者:伊豆山 健夫
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
マクスウェル-ボルツマン分布
マクスウェルボルツマンブンプ
Maxwell-Boltzmann's distribution
J.C. Maxwellによって最初に導かれ,ついでL. Boltzmannによって一般化された,気体分子の状態を表す物理量(たとえば,分子の速度,エネルギーなど)の分布をいう.ボルツマン統計によると,互いに区別可能で,かつどのエネルギー準位にいてもかまわないような粒子N個のうち,縮重度 gj のエネルギー準位 εj に存在する粒子の個数 Nj は,
Nj = Ngje-εj /kT/ 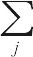 gje-εj /kT
gje-εj /kT
のように表される.ここで,e-εj /kT をボルツマン因子という.縮重が無視できるとき,熱平衡にある理想気体について,質量mの気体分子の運動速度vの分布は,
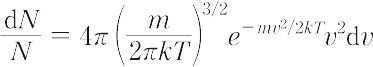
となる.これをマクスウェル-ボルツマンあるいは単にマクスウェルの速度分布則という.
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
Sponserd by 
マクスウェル=ボルツマン分布
マクスウェル=ボルツマンぶんぷ
Maxwell-Boltzmann distribution
古典的な気体分子運動論において理想気体が熱平衡状態で示す確率分布。ある分子がエネルギーεで運動している確率は,気体の絶対温度を T ,ボルツマン定数を k とすると, exp (-ε/kT) に比例する。εは一般に外力による位置エネルギーも含む。外力のない場合は運動エネルギーだけとなり,速度の各成分が u と u+du ,v と v+dv ,w と w+dw の間にある単位体積あたりの分子の数は次のように表わされる。
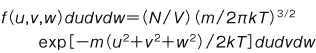 ただし m は分子の質量,N は分子の総数,V は気体の占める体積である。この f(u,v,w) をマクスウェル=ボルツマン分布またはマクスウェル分布という。この分布は分子が古典統計に従うときにのみ成り立ち,量子統計に従うときにはフェルミ=ディラック分布またはボース=アインシュタイン分布になる。
ただし m は分子の質量,N は分子の総数,V は気体の占める体積である。この f(u,v,w) をマクスウェル=ボルツマン分布またはマクスウェル分布という。この分布は分子が古典統計に従うときにのみ成り立ち,量子統計に従うときにはフェルミ=ディラック分布またはボース=アインシュタイン分布になる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内のマクスウェル=ボルツマン分布の言及
【温度】より
…熱運動は温度が高くなると激しくなる。希薄な気体の場合,個々の分子はいろいろな速度,したがって運動エネルギーで運動しているが,ある一つの分子がエネルギーEをもつ確率は,気体の温度をT(K)とすると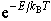 に比例し(マクスウェル=ボルツマン分布),平均のエネルギーは単原子分子の気体の場合3/2kBTで与えられる。ここでkBはボルツマン定数と呼ばれ,kB=1.38×10-23J・K-1に等しい。…
に比例し(マクスウェル=ボルツマン分布),平均のエネルギーは単原子分子の気体の場合3/2kBTで与えられる。ここでkBはボルツマン定数と呼ばれ,kB=1.38×10-23J・K-1に等しい。…
【統計力学】より
…この方法はポテンシャルをもつ外力が分子に作用している場合へも拡張できて,Aは分子1個の運動エネルギーにポテンシャルエネルギーを加えたものとすればよい。このようにして得られた熱平衡状態における分子の各状態の確率分布を[マクスウェル=ボルツマン分布]と呼ぶ。ボルツマンはさらに分子間衝突を具体的に取り扱わなくてよい一般論に触れている。…
※「マクスウェル=ボルツマン分布」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
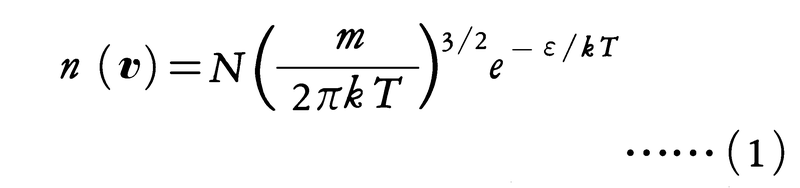
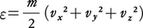 は粒子の運動エネルギーであり,mは粒子の質量,kはボルツマン定数である。(1)の速度分布をマクスウェルの速度分布則という。これは最初J.C.マクスウェルによって与えられたものであり,のち,L.ボルツマンによって一般化された。量子統計力学では(1)に対応するものは,粒子間の相互作用を無視したときのフェルミ粒子系のフェルミ=ディラック分布やボース粒子系のボース=アインシュタイン分布である。これらの分布関数はいずれも古典極限(2πmkT/(N/V)2/3≫h2)ではe⁻ε/kt・eμ/ktとなり,これはマクスウェル=ボルツマン分布にほかならないことがわかる。ここで,hはプランク定数,Vは粒子を入れた容器の体積,μは化学ポテンシャルである。またフェルミ=ディラック分布やボース=アインシュタイン分布は1粒子状態への分布で,定義からすると,速度分布関数に(h3/m3V)を乗じたものに対応していることに注意する。また,
は粒子の運動エネルギーであり,mは粒子の質量,kはボルツマン定数である。(1)の速度分布をマクスウェルの速度分布則という。これは最初J.C.マクスウェルによって与えられたものであり,のち,L.ボルツマンによって一般化された。量子統計力学では(1)に対応するものは,粒子間の相互作用を無視したときのフェルミ粒子系のフェルミ=ディラック分布やボース粒子系のボース=アインシュタイン分布である。これらの分布関数はいずれも古典極限(2πmkT/(N/V)2/3≫h2)ではe⁻ε/kt・eμ/ktとなり,これはマクスウェル=ボルツマン分布にほかならないことがわかる。ここで,hはプランク定数,Vは粒子を入れた容器の体積,μは化学ポテンシャルである。またフェルミ=ディラック分布やボース=アインシュタイン分布は1粒子状態への分布で,定義からすると,速度分布関数に(h3/m3V)を乗じたものに対応していることに注意する。また,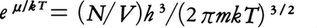 に注意すると,古典極限におけるマクスウェル=ボルツマン分布への移行が明らかになろう。
に注意すると,古典極限におけるマクスウェル=ボルツマン分布への移行が明らかになろう。

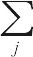 gje-εj /kT
gje-εj /kT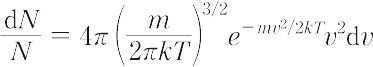
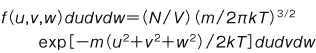 ただし m は分子の質量,N は分子の
ただし m は分子の質量,N は分子の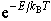 に比例し(マクスウェル=ボルツマン分布),平均のエネルギーは単原子分子の気体の場合3/2kBTで与えられる。ここでkBはボルツマン定数と呼ばれ,kB=1.38×10-23J・K-1に等しい。…
に比例し(マクスウェル=ボルツマン分布),平均のエネルギーは単原子分子の気体の場合3/2kBTで与えられる。ここでkBはボルツマン定数と呼ばれ,kB=1.38×10-23J・K-1に等しい。…