エネルギー(読み)えねるぎー(その他表記)energy
精選版 日本国語大辞典 「エネルギー」の意味・読み・例文・類語
エネルギー
- 〘 名詞 〙 ( [ドイツ語] Energie )
- ① 基本的な物理量の一つ。仕事をすることができる能力、またはその量。最初は物体が仕事をなしうる力学的エネルギーのみが考えられていたが、次第に熱、電磁気、光、質量など間接的なものにも拡大された。大きさは、そのエネルギーがなくなるまでの間にする仕事の量で表わされる。単位はエルグ、ジュールなど。
- [初出の実例]「較(や)や中等以上を占めたる人すらも『モレキエールス』や『ヱネルギー』の何物たるを知らざるも」(出典:戦後の文学(1895)〈内田魯庵〉)
- ② 人間の活動、行動の源となる力。個人の肉体的な行動の源となる力や、多くの人間による社会的な活動、運動のもととなる力などをいう。精力。活気。
- [初出の実例]「詩歌は人生なり、人生の主粋は都会に在り、都会は人生の中心にしてエネルギーなり」(出典:時事新報‐明治四一年(1908)八月一二日)
- ③ 「エネルギーしげん(━資源)」の略。
日本大百科全書(ニッポニカ) 「エネルギー」の意味・わかりやすい解説
エネルギー
えねるぎー
energy 英語
énergie フランス語
Energie ドイツ語
一般に、物体が他の物体に対して仕事をすることができる状態にあるとき、その物体はエネルギーをもっているという。どんな物理系でも、外界となんの交渉ももたずに、限りなく仕事をし続けることはできない。これは経験の教える大原理であって「第1種永久機関の不可能の原理」とよばれる。ここで「仕事」ということばは物理学に特有の意味で使われている。
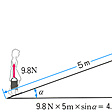
一つの物理系Aが他の系Bに力Fを及ぼして着力点を力の方向に距離lだけ動かしたとき、AはBにFlだけの仕事をしたという。もし着力点が力と角θ(シータ)をなす方向に動いた場合にはFlcosθだけの仕事をしたという。人が9.8ニュートン(1キログラムの物体に作用して1m/s2の加速度を生じさせる力を1ニュートンという。ニュートンはNで表す)の力で荷物をぶら下げて水平面と角α(アルファ)をなす斜面を5メートル歩いたとすれば、力の方向と移動の方向とは90゜-αの角をなすから、この移動では
9.8N×5m×sinα=4.9sinαN・m
だけの仕事をしたことになる()。N・mをまたJと書きジュールと読む。ジュールは仕事の単位であるが、またエネルギーの単位でもある。
[江沢 洋]
いろいろなエネルギー
力学的エネルギー
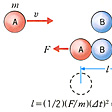
質量mの物体を物理系Aとし、これが無重力の空間を速さvで右向きに走っているとする。これが物理系B(同じく質量mの物体)に衝突し、Bを一定の力Fで押していくなら、その反作用としてAはBから左向きに一定の力Fを受け、速さを単位時間当りF/mずつ減じて、時間Δt=v/(F/m)ののちには止まってしまう()。この時間にAが走る距離は
l=(1/2)(F/m)(Δt)2=(mv2/2)/F
であるから、AがBにする仕事はFl=(1/2)mv2である。Bは同じだけの仕事をされて速さvで走り出す。Aは他のどんな方法で別の物理系に働きかけても、これ以上の仕事はできないことが証明できる。実際、過程Γ′でそれができたとしたら、その仕事の一部を使って、Aに力Fを右向きに時間Δtだけ働かせ、Aをもとの速さにする過程Γと交互にΓ′、Γ、Γ′、Γ……のように繰り返すことで永久機関がつくれるはずである。ところが、前述の「第1種永久機関の不可能の原理」から、それはありえない。したがって、速さvで走る質量mの物体はちょうど(1/2)mv2のエネルギーをもつことがわかる。これを運動エネルギーという。この物理系Aが孤立している場合、すなわちなんの力も受けない場合には、物体mの速度は変わらないから、物理系Aのエネルギーはいつまでも一定のままである。
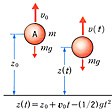
次に、物体mが鉛直下向きの重力mgが働く場を運動するとして、ここでも物体mを物理系Aにとる。ある瞬間に質点mの高さがz0、速度が鉛直上向きにv0であったとすれば、時間tののちには、高さは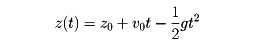
となり、速度はv(t)=v0-gtに変わる。したがって物理系Aのエネルギー(質点Aの運動エネルギー)も
に変わる()。他方、物体mが上向きにz(t)-z0の距離を動く間、つねに重力場は下向きにmgの力をmに及ぼしていたため、仕事-mg[z(t)-z0]をした。mの移動によりこれだけ重力場のエネルギーが減っていると考えられる。いいかえれば重力場のエネルギーは、+mg[z(t)-z0]だけ増えている。そこで今度は物体mと重力場とをあわせて一つの物理系A1として、それぞれのエネルギーの増分を足し合わせてみると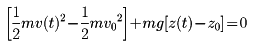
となる。あるいは変形して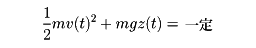
とすることもできる。左辺はつねにt=0における値に等しいからである。ここで付加されたmgzを物体mと重力場の相互作用エネルギーとよぶ。それに物体の運動エネルギーを加えたもの、つまり孤立系A1の全エネルギーが時刻tによらず一定なのである。なお、mgzをしばしば物体mの位置エネルギーともよぶが、これをもつのは物体と重力場をあわせた系であって、物体mだけではないということを忘れてはならない。
一般に、物体mが力の場の中を任意の点Pから任意の点Qまで移動するとき、場のする仕事が始点Pと終点Qとの位置のみで定まって途中の経路によらないとき、この場は保存力の場であるという。そしてPを固定し、Qまでの移動で場がする仕事を、Qの位置rの関数とみて-V(r)と書く。そうすると、物体mが位置rにきたときの速度をvとして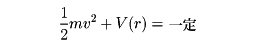
という関係の成り立つことが運動の法則から証明される。そこで物体mについて(1/2)mv2を運動エネルギーとよび、V(r)を位置のエネルギーとよぶ。両者の和が時刻によらず一定であるという前記の関係を力学的エネルギー保存の法則とよぶ。なお、物体が回転もするときには回転運動のエネルギーも運動エネルギーに含めておかなければならない。
[江沢 洋]
熱のエネルギー
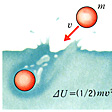
速度vで飛んできた物体mが水の中に飛び込んだとすると、物体は水の抵抗を受けてやがて静止する。このとき水の温度が上がり、実験してみると、あたかも高温の熱源に接触させて熱量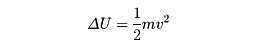
を加えたのと同じことになる。これだけ水の内部エネルギーが増すのである()。そこで物体mと水とをあわせて物理系A2とすれば、これは孤立系となるが、物体の運動エネルギーと水の内部エネルギーの和(系A2の全エネルギー)はつねに一定となる。物体の内部エネルギーは摩擦のように仕事をすることによっても増加させることができる。一般に内部エネルギーUの変化を伴う過程では
(力学的エネルギー)+U=一定
がエネルギーの保存則になる。
温度の高い物体は熱をもつというが、温度はこのように力学的エネルギーの供給によっても上げることができる。内部エネルギーを増す操作のうえからは熱を力学的仕事から区別できるが、いったん物体の中に入って内部エネルギーとなってしまえば両者の区別はできない。
[江沢 洋]
その他のエネルギー
エネルギーには以上にあげたもののほか、音波などの波動のエネルギーや電磁場のエネルギーなど多くの種類が知られている。新しい現象に出会えば、エネルギー保存則を成り立たせるために新しい種類のエネルギーを考えねばならなくなることもある。これまでエネルギーの概念は、このようにして保存則を成り立たせるように拡張されてきた。今後もつねにこれが可能であるという主張をするのがエネルギー保存則の実質的内容である。
全世界の海洋をエネルギー源として利用することはエネルギー保存則だけからは可能であるようにみえ、したがって永久機関に近いものがつくれそうに思われる。このように、一つの熱源から熱をとり、その全部を仕事に変え、それ以外になんの変化も残さないようにする装置を第2種永久機関とよぶが、それをつくることは実際は不可能である(熱力学第二法則)。他方、力学的エネルギーの場合はその全部を仕事に変えることができる。このようにエネルギーには種類により利用しやすさに差がある。その差はエントロピーで測ることができる。エントロピーの低い状態にあるエネルギーは秩序だっていて利用しやすいが、エントロピーの高い状態のエネルギーは、気体分子の乱雑な運動に代表されるように方向性がなく、利用しにくい。
[江沢 洋]
微視的世界におけるエネルギー
相対性理論によれば、物理系のエネルギーEはE/c2だけの質量として現れる(cは光速3×108m/s)。粒子の速度が増すと運動エネルギーの増加に伴って質量が増すのは、その例である。こうしてエネルギーの保存則と質量の保存則は統一され、同じことを別の表現で述べているにすぎなくなった。物体が静止しているときの質量を静止質量とよび、それにc2を掛けた値を静止エネルギーという。物体を熱すれば静止質量が増す。しかし、系のエネルギーが1ジュール増しても質量は1.1×10-15kgしか増さないので、日常の現象ではエネルギーと質量は無関係な別ものとして扱われる。他方、核物理的な現象では電子と陽電子(質量の合計9.1×10-31kg×2)が対(つい)消滅して光(エネルギー1.6×10-13J)に変わるといった転化過程が普通におこる。この場合にも質量が消えるわけではなく、光を容器にとらえれば質量がそれだけ増しているのがわかるはずで、質量がエネルギーに変わったというのは正しくない。質量が姿を変えただけである。
陽子(質量1.673×10-27kg)92個と中性子(質量1.675×10-27kg)143個が結合するとウラン235の原子核ができるが、その質量は3.902×10-25kgしかなく、陽子と中性子の質量の和より3.2×10-27kgも軽い。これは、陽子と中性子はばらばらにいるときより、互いに引き合って原子核をつくっているほうがエネルギーが下がるからであり、その差を結合エネルギーという。同様のことは他の原子核でもおこっている。ウラン235は中性子でたたくと、大きさが同じくらいの二つの核に分裂し、同時に2個または3個の中性子が飛び出す。この分裂後の質量の総計はウラン235の質量より小さい。その差Δmに相当してΔmc2だけのエネルギーが解放され核分裂破片の運動エネルギーやガンマ線として現れることになる。これがいわゆる核エネルギーである。しかし、この場合にも全体を容器に収めて全質量を測ることができたとすれば、核分裂の前後で質量は変わらないことがわかるはずである。核エネルギーは重水素のような軽い核が融合するときにも解放される。
原子核に電子が結合して原子をつくるとき、また原子が結合して分子をつくるときにも結合エネルギー分だけ質量が減るはずであるが、それぞれ原子の質量の1億分の1、10億分の1程度にすぎないので普通は問題にならない。
光はエネルギーのかたまりとして物質により放出または吸収される。このかたまりを光子という。そのかたまりの大きさは光の振動数ν(ニュー)で決定しhνである。ただしhはプランク定数6.6×10-34J・sである。光子のエネルギーは赤い光(ν~4.5×1014s-1)では3.0×10-19J程度であるのに対し、紫色の光(ν~7.5×1014s-1)では5.0×10-19J程度になる。赤外線にいくら当たっても日焼けしないが紫外線に当たると日焼けするのは、前者の光子のエネルギーが、日焼けの化学反応をおこすには小さすぎるためである。
電子が原子くらいの大きさの領域に閉じ込められると特定のエネルギーの値しかとれなくなる。その特定の値をエネルギー準位とよぶ。たとえば、水素原子の電子のエネルギー準位は
-2.18×10-18J/n2 (n=1,2,……)
である。この電子は、原子核の近くを回るほどエネルギーが低くなるはずであるが、電子のエネルギー準位はn=1の場合に最低値をとり、これ以下になることはないため、核に落ち込むことができない。これは他の原子でも同様で、つまり、エネルギー準位の存在が原子を崩壊から守り、物質の安定性を保証している。エネルギー最低の準位を基底準位とよび、対応する運動状態を基底状態とよぶ。電子を一つの準位から、より高い準位に上げることを励起するという。たとえば、基底準位(n=1)から第一励起準位(n=2)への励起には-2.18×10-19J×(2-2-1-2)だけの励起エネルギーが必要である。これに等しいhνの光を当てれば励起ができる。n=1の準位からn→∞への励起エネルギーは、原子から電子をはぎとるのに必要なエネルギーで、イオン化エネルギーとよばれる。
一般に一つの物理系について時刻tとエネルギーEを同時に正確に測ることは不可能で、それぞれの誤差Δt、ΔEの間に不確定性関係ΔE・Δt≧ħ(ħは、プランク定数hを2πで割ったもの。つまりħ=h/2π)がある。その著しい例は、原子の励起状態の寿命τ(タウ)と対応するスペクトル線の自然幅Δνとの関係Δν=1/(2πτ)である。また素粒子の寿命τと質量の幅との間にも同様の関係ΔMc2~ħ/τがある。
[江沢 洋]
エネルギー概念の成立
エネルギー概念が物理学において確立されたのは、通例では19世紀なかば、すなわち1840年代のマイヤー、ジュール、ヘルムホルツらによるエネルギー保存則提起の時期とされている。ただし、当時知られる限りのすべての形態のエネルギーに対して、ことばとして初めてエネルギーとよんだのはランキンであり、1850年代に入ってからである。以上の時期に先だつエネルギー概念導入の過程は、まさに力学の成立・展開とともに、カテゴリーとしてのエネルギー概念を一歩一歩明確化させる過程として進められた。その後、以上の保存則成立期以降において、力学的エネルギー、熱エネルギー、電磁気的エネルギーなどが統一的にとらえられるようになり、さらに、20世紀に入って相対論により質量とエネルギーの同等性が提起される。このようにみてくると、物理学の発達の歴史は、まさに、エネルギー概念の拡大・展開の歴史でもあるということができよう。そしてエネルギー保存則は、つねに、新たな形態のエネルギーをそのなかに包摂しながら、より普遍的かつ基本的な自然法則として維持され、今日に至っている。
歴史上、最初に「仕事の量」を問題にすることで、エネルギー概念への端緒を与えたのはレオナルド・ダ・ビンチであり、てこ、滑車などの器具を用いた場合、仕事の量を増加させることはできないと指摘した。ダ・ビンチの業績は物理学としての力学研究の先駆ともなるものであった。16世紀末から17世紀初めにかけてガリレイ、ケプラーによる力学、天体運動に関する研究が進む。物体が落下に際し、もとの位置に戻るのに必要な速度を得るという事実は、ガリレイにより実験的にみいだされた。以上の事実に対して、「宇宙のなかにつねに同じ量の『運動』を保存している」(『哲学原理』1644)と述べて、初めてエネルギーについての体系的な説明を与えようとしたのはデカルトである。デカルトにおけるこの「運動」は今日の意味では運動量であり、これは「運動量保存則」を述べている。そして、デカルト派は「力の測度」は「運動の量」mvであるとした。これに対してライプニッツは、「力の測度」はmv2であることをガリレイの実験結果に基づいて主張した(1686)。ライプニッツが「活力」vis vivaと名づけたこの「力」は、今日の意味では1/2の係数を別にして運動エネルギーそのものである。ニュートンは1687年『プリンキピア』を世に出しているが、力、運動量、エネルギー概念に関する当時の混乱に巻き込まれることを避けるためか、そのなかでエネルギー概念については何も述べていない。「力の測度」は何であるかをめぐってのこのライプニッツ派―デカルト派の論争は18世紀なかばころまで続く。この論争に決着をつけ、力学におけるそれぞれの量の意義を明らかにすることは、ダランベールらによってなされ、のち、T・ヤングはmv2に対して初めてエネルギーということばをあてた(1807)。
19世紀に入って、産業革命の全ヨーロッパ的展開による蒸気機関の普及と鉄道の発達は、エネルギー保存則成立への第一の前提となった。蒸気機関車はエネルギー転換装置の典型として当時の人々の目に映った。そのなかで熱力学が成立する。第二の前提条件は近代化学の成立、生物学の展開であり、化学、生物学の面からエネルギー転換に関心が寄せられた。第三は電磁気学の成立である。J・R・von・マイヤーは、船医としての経験から、熱帯地方では船員の血液が赤みを増すことに気づき、そこから、一般原理としてエネルギー保存則を提起した(1842、1845)。ジュールは電流の熱作用についてのジュールの法則をみいだし(1840)、分銅の落下による仕事で電磁誘導を利用して電流を生じさせ、その電流による発生熱量の測定から、熱の仕事当量を初めて定めた(1843)。さらに、1845年には有名な羽根車の実験で直接それを求めている。マイヤー、ジュールに次いで、エネルギー保存則の解析的表現を与えて定式化したのはヘルムホルツである(1847)。以上のように、1840年代を通じての明確な形での保存則の提起・確立によって、さらに19世紀後半から20世紀にかけての新たな諸科学・技術学の登場と成立過程を通じて、エネルギー概念は物理学のみならず、全自然科学体系にとっての基本カテゴリーとしての位置を占めることになる。しかしながら、当時はマイヤーもヘルムホルツもエネルギーを「力」とよんでいた。これは、先に述べた問題がなお尾を引いていたとみられる。エネルギーの語がことばとして定着するのは、J・J・トムソン、ランキン以降である。
以上のエネルギー保存則の成立期は同時に熱力学の興隆期であり、エネルギー保存則は熱力学第一法則としてそのなかに位置づけられる。いいかえれば第1種永久機関の不可能性を意味するものとなる。そして、熱機関の熱効率を規定する法則として熱力学第二法則がみいだされ、これは第2種永久機関の不可能性を示すとともに、エントロピー概念を提起する。こうしてエネルギーの転換と移動を規定する科学としての熱力学の成立は、熱機関の技術的展開と並行し、それに支えられて進められる。1860年前後にマクスウェルにより電磁気学の体系化が行われ、1860年代から1870年代にかけて、E・W・von・ジーメンス、グラム、アルテネックらの努力で、力学的エネルギーを電気的エネルギーに転換する機関としての発電機が実用化され、1882~1883年、エジソンによる中央火力発電所の建設・操業開始(ニューヨーク、ロンドン)は電気エネルギー利用を社会的な形で位置づけた。ここに電気の時代が始まる。
[荒川 泓]
『朝永振一郎編『物理学読本』(1969・みすず書房)』▽『有光敏彦著『初等物理シリーズ3 エネルギーと熱』(1989・培風館)』▽『小山慶太著『永久機関で語る現代物理学』(1994・筑摩書房)』▽『荒川泓著『エネルギー・3つの鍵』(1996・北海道大学図書刊行会)』▽『伊東弘一・大岡五三実・武田洋次・片山紘一・町井令尚著『エネルギー工学概論』(1997・コロナ社)』▽『岡部豊・堂寺知成著『エネルギーと熱』(1998・放送大学教育振興会)』▽『日本原子力学会編『ミクロ科学とエネルギー』(1999・コロナ社)』▽『藤田秀臣・加藤征三著『機械システム入門シリーズ10 熱エネルギーシステム』(1999・共立出版)』▽『茅陽一・鈴木浩・中上英俊・西広泰輝・村田稔・森信昭編『エネルギーの百科事典』(2001・丸善)』▽『藤井康正・茅陽一著『岩波講座現代工学の基礎5 エネルギー論』(2001・岩波書店)』▽『阿部龍蔵著『エネルギーと電磁場』(2002・裳華房)』▽『江沢洋著『量子力学1、2』(2002・裳華房)』▽『江沢洋著『相対性理論とは?』(2005・日本評論社)』▽『成田正邦著『量子エネルギー工学入門』(2003・現代工学社)』▽『R・P・ファインマン著、江沢洋訳『物理法則はいかにして発見されたか』(岩波現代文庫)』▽『池内了著『私のエネルギー論』(文春新書)』
改訂新版 世界大百科事典 「エネルギー」の意味・わかりやすい解説
エネルギー
Energie[ドイツ]
英語ではエナージーenergyという。
エネルギー概念の発展
仕事と力学的エネルギー
エネルギーの概念が確立したのは19世紀後半であるが,これと深いかかわりをもつ仕事の概念の歴史はずっと古く,すでに紀元1世紀ごろ,アレクサンドリアのヘロンは,てこや滑車などの機械による仕事について,力に関する利得が速さまたは移動距離に関する損失で帳消しにされるということを述べている。これは現在仕事の原理と呼ばれるもので,詳しくいうと次のようになる。われわれはてこのような機械を利用して機械が物体に大きな力を及ぼすようにすることはできるが,その力(力の物体の移動方向の成分)と移動距離との積=〈機械のする仕事〉は,機械に対してわれわれの加える小さな力と必要な大きな移動距離の積=〈われわれのする仕事〉に等しくなり,(機械に摩擦がなければ)仕事の量は結局機械を用いなかったときとまったく同じになる。このこと,すなわち機械は仕事を伝達するものであって生みだすものではないということもレオナルド・ダ・ビンチの時代にははっきり認識されていた。例えば,S.ステフィンはこれを自明のこととして用いて,力の合成の平行四辺形則を証明している。
しかし,エネルギーの概念の萌芽となった運動エネルギーに関する考察を初めて試みたのは,やはりG.ガリレイであった。彼は1600年ごろ,木材の上に立てた釘の頭に金づちの頭よりずっと重い物を載せても釘は木の中に入らないが,金づちを振り上げて打つだけでなぜ釘は楽に木材に打ち込まれるのかを問題にし,運動する物体には何か固有の“ちから”があると考えた。これについてR.デカルトは44年の著書で,衝突現象で運動量mv(mは物体の質量,vは物体の速度)が保存されることに注意し,全宇宙における総運動量が不変であり,運動量こそが運動する物体のもつ“ちから”であると主張した。デカルトやその支持者たちの考え方からすると,運動や運動の変化の原因としての(外から働く)力は運動量の変化として測られることになる。この意味で彼らはI.ニュートンの運動の法則のまさに一歩手前まで到達していたといってよい。これに対し,86年にG.W.ライプニッツは当時の常識であった〈運動する物体のもつ力は物体に固有のものでなければならぬ〉という考えから,mv2という量こそがこの“ちから”を表し,宇宙全体で保存されるのはこの量の総和であるとし,静力学のつり合いで現れる“死んだ力vis mortua”に対して,これを“活力vis viva”と呼んだ(なお,C.ホイヘンスもこれに先だって複合振子の取扱いでmv2という量を使ったが,とくにその重要性を強調することはしなかった)。ライプニッツの議論は次のようなものであった。質量mを4hの高さだけもち上げるときと,質量4mを高さhだけもち上げるときとでは同じ“ちから”(いまの言葉では仕事)がいる。したがってmが4hだけ落下するときの“ちから”は4mがhだけ落下するときのそれと同じはずである。実際4mがhだけ落下したときもつ速さをvとすると,両方の場合について“活力”は等しくなる。落下点での前者の場合の速さは2vになり,m(2v)2=4mv2となるからである。しかしこのとき運動量についてはm2v≠4mvとなって同じにはならない。この後,約半世紀にわたってデカルト派とライプニッツ派の間に“ちから”の解釈に関する論争(活力論争,vis viva論争)が続いた。しかし,J.L.R.ダランベールが1743年の著書《力学》の中で,デカルトの考えた“ちから”は力の時間積分であり,ライプニッツの“活力”は力の位置座標についての積分(つまり仕事)であることを指摘するにおよび,この論争もしだいにおさまっていった。なお,83年N.L.S.カルノーは“活力”の保存という概念をすでに暗示しているが,彼の業績は19世紀半ばまで一般には知られなかった。
エネルギーという言葉は,ギリシア語energeia(接頭語en=内部に+ergon=仕事)に由来し,〈物体内部に蓄えられた仕事をする能力〉という意味で,T.ヤングがそれまでの“活力”に代わるものとして用いた(1807)が,1850年代初期にW.J.M.ランキンやW.トムソン(ケルビン)らがこの語を意図的に再使用し始めるまでは一般には使われなかった(英語ではforce,ドイツ語ではKraftなどがそれに当てられていた)。“仕事”を現在の意味(力×移動距離)に定義し,活力の代りに運動エネルギーT=1/2mv2を用いて,その変化高ΔTと物体に働く力のする仕事Wの関係をΔT=Wの形に与えたのは,G.G.コリオリである(1829)。物体に働く力が重力の場合,そのする仕事には次の特徴がある。すなわち重力の働いているところで,h1という高さからh2という高さまで物体が動くとき,重力のする仕事Wはmg(h1-h2)のように(gは重力の加速度),位置だけの関数V=mghの場所1での値と場所2での値の差V1-V2の形に表され,どんな経路を通ってどんなやり方で1から2へ移すか,ということには依存しない。このような性質をもった力を保存力という。重力は保存力である。保存力のとき,前述の関係は⊿T=T2-T1=1/2mv22-1/2mv12=W=V1-V2(v1,v2は場所1および2での物体の速さ)となるから,T1+V1=T2+V2≡E(=一定)が成り立つ。Vは位置エネルギー,T+Vは力学的エネルギーと呼ばれる。上式は保存力のときは,位置エネルギーまで含めた力学的エネルギーが物体の運動の際,状態が変わっても変化しないという(力学的)エネルギー保存の法則(エネルギー保存則)である(実質的にはJ.L.ラグランジュによって1811年に与えられた)。
熱とエネルギー
力学的エネルギーの保存則は現実には満たされない場合が多い。現実の運動にはかならず摩擦や粘性抵抗などが関係し,保存力以外の力(非保存力)を考えねばならないからである。例えば粗い斜面を物体が滑り降りるとき,力学的エネルギーは保存されず減少する。その減り高ΔEは物体が摩擦力に逆らってした仕事Wに等しく,後者は摩擦熱の発生という形で失われることになる。したがってこのような場合にもエネルギー保存則を成り立たせようとすると,力学的仕事だけでなく熱まで含めて考えねばならない。熱については18世紀ごろまでは熱素(カロリックcaloric)というある種の重さのない物質であるという考えがあり,A.L.ラボアジエなどはこれを元素表の中に記したほどであった。N.L.S.カルノーはこの熱素説に基づいて,当時発達途上にあった蒸気機関の原理を,熱素の流れによって説明した(1824)。一方,すでに19世紀初めに,アメリカの技師W.トムソン(のちのランフォード伯)は,大砲の砲身を削っていくといくらでも熱を発生することから熱の物質説に反対し,熱が何か物質内の運動に起源をもつものであることを主張した。1840年ごろ,ドイツの医師J.R.vonマイヤーは,瀉血(しやけつ)の際の患者の血の色がヨーロッパと熱帯の国々とで異なることに暗示され,力学的現象と熱現象を合わせて(さらにはもっと一般に他の形のエネルギーも含めて)エネルギー保存則が成り立たねばならないことを指摘した。実際,彼はそれに基づいて観測された気体の定圧,定積比熱の値の差から,(ジュールの実験を知らずに)理論的に熱の仕事当量の値のおおよその値を見積もることに成功している。同じころイギリスのJ.P.ジュールは,一定量の力学的仕事をすればどんな物質に対してもどんな方法ででもかならず一定の熱量が得られるはずだと考え,おもりの降下に伴う羽根車の回転によって容器内の液体をかき混ぜて熱を発生させ,この熱とおもりになされた仕事とを比べて,実験的に熱量1calが仕事4.19Jに当たることを確かめた(この数字が熱の仕事当量Jで,正しくはJ=4.186J/cal)。つまりW(J)の仕事がすべて熱Q(cal)に変わったとするとW=JQである。最後にH.L.F.vonヘルムホルツも1847年に一般的な立場から,すべて仕事をすることのできる能力,すなわちエネルギーが電磁気現象も含めどんな現象においても保存されることを論じ,一般的な保存則の成立を主張した。それによると力学的現象に熱現象を含めた範囲でのエネルギー保存則,すなわち熱力学の第1法則は次の形になる。いまある物体に外部からW(J)の力学的な仕事を加え,またQ(cal)の熱を流入させる。これによって物体の状態が1から2に変化したとする。このとき,
ΔU≡U2-U1=W+JQ ……(1)
が成り立つ。熱力学の場合は対象とする物体全体としての運動はふつう考えないから,U2-U1は物体の内部エネルギーUの変化を表す。ただし内部エネルギーというのは熱運動をしている物体中の原子やイオンの力学的エネルギーの総和(イオン間の電磁気的エネルギーも含める)のことである。(1)式の右辺の仕事や熱も結局は外界の力学的エネルギーや内部エネルギーの減少でまかなわれているのだから,外界の変化まで含めてしまうと(1)式は変化の前後でエネルギーの総和が変わらないというエネルギー保存則を表している。先に述べたようにマイヤー,ヘルムホルツが電磁気現象,化学変化なども含め,物理学全般にわたりすべての形態のエネルギーが保存されることを明らかにしたのに伴い,エネルギーは物理学のもっとも重要な基礎的概念として確立されることになった。
→エネルギー論
エネルギーの単位
エネルギーの単位には仕事と同じ単位を使う。MKS単位系では,仕事の単位は〈力の単位〉×〈長さの単位〉でN・mとなり,これをジュール(J)と呼ぶ。エネルギーの変化率は仕事率と同じくワット(W=J/s)で測られる。エネルギーの単位として原子物理学では電子が1Vの電位差で加速されたとき得るエネルギー,電子ボルト(eV)を用いることが多い。1eV=1.60×10⁻19Jである。
エネルギーのいろいろな形態
力学的エネルギー
運動エネルギーと位置エネルギーの和,すなわち力学的エネルギーは物体の状態を指定する変数(位置,速度,回転を伴うときは角速度など)の関数であって,物体の運動が行われている間一定に保たれる。しかし上にも述べたとおり,非保存力が働いていると,これに逆らって仕事をし熱を発生させるから,力学的エネルギーはその分だけ減少することになる。このような非保存力が現れるのは,われわれが原子のスケールでの物質の構造にまで立ち入らず,微視的に見たときの相互作用や熱運動をしている原子間のエネルギーのやり取りの結果生じたエネルギー(内部エネルギー)の増加を,巨視的な立場で非保存力の存在と,それに対してなした仕事の結果と見なすからである。
内部エネルギー
簡単には物質を構成している原子(またはイオン)の熱運動の(力学的・電磁気的)エネルギーの総和と考えればよい。気体では,気体分子の運動エネルギー(多原子分子のときは回転のエネルギーや振動のエネルギーも含む)の総和。単原子理想気体では気体原子の平均運動エネルギーは絶対温度に比例する。液体,固体では構成原子や分子間の力による位置エネルギーも無視できず,これを合わせた全力学的エネルギーが内部エネルギーとなる。位置エネルギーが関係するため,この場合内部エネルギーは温度だけでなく体積の関数にもなる。しかしいずれにせよ,物質の内部エネルギーはやはり物体の状態を指定する変数(今の場合温度と体積)の関数として,状態ごとに決まった値をとる“状態量”である。一般に温度を上げれば内部エネルギーは増加する。逆に内部エネルギーが増えれば温度は上がる。これが熱の発生である。その意味で熱をもつというより内部エネルギーをもつといういい方のほうが正しい。しばしば熱をエネルギーの一つの形態だというが,これも厳密ではない。エネルギーは状態量であって,その状態でとる値の決まった量であるが,熱というのはかならず状態の変化に伴って出入りするもので,仕事と同じように状態の変化のさせ方を具体的に指定して初めて値の決まる量である。しかも(1)式で見るとおり,熱または仕事というものは,単独で切り離してエネルギーという資格を与えることのできる量ではなく,両方合わせて初めてその資格の生ずるような量なのである。
→熱
電磁場のエネルギー
充電したコンデンサーの両極をつないで放電するとパチッと音がして火花が飛ぶ。これは電気を蓄えたコンデンサーにエネルギーが蓄えられていることを示す。実際,電気容量Cのコンデンサーに0から充電してQの電荷をためるには,Q2/(2C)の仕事が必要なことを示すことができる。これがこの状態でコンデンサーのもつエネルギーである。ところで場の考え方では,このエネルギーをコンデンサーの電荷がつくり出した電場に蓄えられているものと見なす。この考えに従って調べてみると,電場がEの場所には,単位体積当りのエネルギー(エネルギー密度)として,ちょうどwe=1/2ε0E2(ε0は真空の誘電率)が蓄えられていると考えればよいことがわかる。同様に電流の流れているコイルにもエネルギーが蓄えられている。(自己)インダクタンスLのコイルの電流を0からIまで増やすには,途中自己誘導によって生ずる逆起電力に逆らって,全体で1/2LI2だけの仕事をしなければならないからである。この場合も場の考え方に従ってコイルのまわりの磁場を調べてみると,磁場の強さHの場所には密度wm=1/2μ0H2(μ0は真空の透磁率)のエネルギーが蓄えられているとしてつじつまが合う。一般に電荷や電流があって電磁場ができているとき,そのエネルギーはまわりの空間にエネルギー密度w=1/2(ε0E2+μ0H2)で分布していると考えることができる。これが電磁場のエネルギーである。この場のエネルギーについても,全空間で考えると〈電磁場に蓄えられた全エネルギーの減少率〉=〈仕事や熱などで消費される電力〉というエネルギー保存則が成り立つ。
光のエネルギー
光は電磁波であり,電磁波というのは電場・磁場の振動している状態だから,光のエネルギーというのも電磁場のエネルギーである。電磁気学によれば光の電場の振幅をE0とすると,光の定常波が立った状態での電磁場のエネルギー密度(の時間平均)wは1/2ε0E02となる。したがって光のエネルギーは振幅E0が大きいほど大きくなる。しかしこの考えは,A.アインシュタインが金属の光電効果を説明するために提出した光量子仮説により大きな変革を受けることになった。それによると振動数νの光はエネルギー量子hν(hはプランクの定数)をもつ。すなわち光のエネルギーはhνというひとかたまりの大きさでやり取りされる。最低のhνのエネルギーをもつ光の状態は光子(または光量子といい,粒子として見た光のこと)が1個ある状態であって,振動数νの光の一般の状態というのは光子が何個かある状態に当たる。単位体積中に光子がn個あるとすると,上の古典電磁気学の光のエネルギーとの関係は,w=1/2ε0E02=nhνとなる。したがってこの考えではE0が大きくなると光子の個数は増えるが,個々の光子のエネルギーhνが変わるわけではない。振動数νの光がhνの整数倍のエネルギーしかとりえないということは,M.プランクが経験的に得たプランクの放射則を根拠づけるために採用した根本的な仮定であった。
エネルギーとしての質量
特殊相対論の出現までは,エネルギー保存則とは別に質量は質量で保存されるものと考えられていた。ところが相対論によると質量m0の物体が速度vで動いているときには,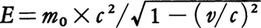 というエネルギーをもつことになる(cは光速)。これはvがcに比べ十分小さい時にはm0c2+1/2m0v2+……と近似できるので,ニュートン力学の運動エネルギー1/2m0v2に静止エネルギーE0=m0c2が加わった形をとっている。このE0がたんにエネルギー表式中に現れる一定の付加定数にすぎないなら,これをエネルギーと呼ぶことにあまり実際上の意味はない。ところが,原子核の世界では確かにエネルギーが質量に変わっている(またはその逆)と考えなければ理解できない現象がある。原子核の質量を精密に測定すると,例えば陽子と中性子がばらばらにあるときより,結合して重陽子になったときのほうがΔm=0.004×10⁻27kgだけ質量が小さい。この質量の減り高(質量欠損という)は陽子と中性子が核力によって結合し,その位置エネルギーの低い状態,つまり全エネルギーの小さな状態に落ち着いたために生じたものと理解できる。この意味で,Δmc2は陽子と中性子の結合エネルギーを与えていることになる。1kgはmc2から計算すると,9.00×1016Jに当たるから,重陽子の結合エネルギーは3.6×10⁻13J(=2.2×106eV)となる。原子の間の化学反応で解放される化学エネルギーは分子当りたかだか数eV程度の大きさだから,この結合エネルギーの膨大さの程度が知れよう。上の解釈によるとこれは結局核力の大きさを反映していると考えてよい。原子核反応の結果質量が減少する場合には,Δmc2だけのエネルギーが反応生成物の運動エネルギー(熱)や光のエネルギーに転化する。このことは定量的に実験でも証明されている。核融合,核分裂などで得られる大きなエネルギーはすべてこのことを利用しているといっても差し支えない(太陽エネルギーも水素原子核の融合の際に放出されるエネルギーだと考えられている)。核反応はこのように質量がエネルギーに変わる例といえるが,逆にγ線による電子・陽電子対の生成のようにエネルギーを利用して物質をつくり出す例もある。これらのことから質量も結局エネルギーの一つの形態であると考えられるようになった。
というエネルギーをもつことになる(cは光速)。これはvがcに比べ十分小さい時にはm0c2+1/2m0v2+……と近似できるので,ニュートン力学の運動エネルギー1/2m0v2に静止エネルギーE0=m0c2が加わった形をとっている。このE0がたんにエネルギー表式中に現れる一定の付加定数にすぎないなら,これをエネルギーと呼ぶことにあまり実際上の意味はない。ところが,原子核の世界では確かにエネルギーが質量に変わっている(またはその逆)と考えなければ理解できない現象がある。原子核の質量を精密に測定すると,例えば陽子と中性子がばらばらにあるときより,結合して重陽子になったときのほうがΔm=0.004×10⁻27kgだけ質量が小さい。この質量の減り高(質量欠損という)は陽子と中性子が核力によって結合し,その位置エネルギーの低い状態,つまり全エネルギーの小さな状態に落ち着いたために生じたものと理解できる。この意味で,Δmc2は陽子と中性子の結合エネルギーを与えていることになる。1kgはmc2から計算すると,9.00×1016Jに当たるから,重陽子の結合エネルギーは3.6×10⁻13J(=2.2×106eV)となる。原子の間の化学反応で解放される化学エネルギーは分子当りたかだか数eV程度の大きさだから,この結合エネルギーの膨大さの程度が知れよう。上の解釈によるとこれは結局核力の大きさを反映していると考えてよい。原子核反応の結果質量が減少する場合には,Δmc2だけのエネルギーが反応生成物の運動エネルギー(熱)や光のエネルギーに転化する。このことは定量的に実験でも証明されている。核融合,核分裂などで得られる大きなエネルギーはすべてこのことを利用しているといっても差し支えない(太陽エネルギーも水素原子核の融合の際に放出されるエネルギーだと考えられている)。核反応はこのように質量がエネルギーに変わる例といえるが,逆にγ線による電子・陽電子対の生成のようにエネルギーを利用して物質をつくり出す例もある。これらのことから質量も結局エネルギーの一つの形態であると考えられるようになった。
→質量 →相対性理論
量子力学的体系のエネルギー
量子力学で扱わなければならない系(原子,分子,固体中の電子や放射の場など)のエネルギーEとして許されるのは,ハミルトニアン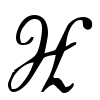 の固有値であって,これは波動関数ψに対するシュレーディンガー方程式
の固有値であって,これは波動関数ψに対するシュレーディンガー方程式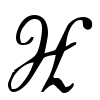 ψ=Eψという固有値問題を解くことによって定められる。ただしハミルトニアン
ψ=Eψという固有値問題を解くことによって定められる。ただしハミルトニアン は系のエネルギーを表す演算子で,古典力学でのエネルギーの表式(粒子の場合,運動エネルギー+位置エネルギー,保存力しか考えない)中の運動量を,対応した座標に関する適当な偏微分演算子で置き換える(例えば運動量のx成分 px→-\(\frac{ih}{2π}\)・\(\frac{∂}{∂x}\))ことによって得られる。古典力学と異なり,定常状態でとりうるエネルギー固有値Eには最低の値があり,対応する基底状態が安定であること,また一般にEとしては連続的な実数値がすべて許されるのでなく,ある範囲ではとびとびの(離散的な)値しか許されなくなるようなことが起こるのは,量子力学的体系の著しい特徴である。したがってエネルギー保存といってもこの許される値の範囲で考えねばならない。例えば原子がある振動数νの光を吸収して(または放出して)エネルギーEnの状態からEmの状態に移ったとすると,Em-En=hν(または-hν)の関係が成り立つ(ボーアの振動数条件)。その他,エネルギーの値がこのように離散的になることの効果は,とくに系の低温での熱的性質(比熱など)に顕著に現れる。ある種の金属の示す超伝導現象なども,体系の連続的なエネルギー状態と基底状態の間にギャップがあることに関連している。
は系のエネルギーを表す演算子で,古典力学でのエネルギーの表式(粒子の場合,運動エネルギー+位置エネルギー,保存力しか考えない)中の運動量を,対応した座標に関する適当な偏微分演算子で置き換える(例えば運動量のx成分 px→-\(\frac{ih}{2π}\)・\(\frac{∂}{∂x}\))ことによって得られる。古典力学と異なり,定常状態でとりうるエネルギー固有値Eには最低の値があり,対応する基底状態が安定であること,また一般にEとしては連続的な実数値がすべて許されるのでなく,ある範囲ではとびとびの(離散的な)値しか許されなくなるようなことが起こるのは,量子力学的体系の著しい特徴である。したがってエネルギー保存といってもこの許される値の範囲で考えねばならない。例えば原子がある振動数νの光を吸収して(または放出して)エネルギーEnの状態からEmの状態に移ったとすると,Em-En=hν(または-hν)の関係が成り立つ(ボーアの振動数条件)。その他,エネルギーの値がこのように離散的になることの効果は,とくに系の低温での熱的性質(比熱など)に顕著に現れる。ある種の金属の示す超伝導現象なども,体系の連続的なエネルギー状態と基底状態の間にギャップがあることに関連している。
エネルギー保存の法則
以上見たように,われわれは運動エネルギーから出発して位置エネルギーを考え,それによって力学的エネルギーの保存則を見いだし,非保存力による熱の発生をも保存則にとり入れられるよう内部エネルギーの概念を導入し,熱と力学的仕事の両者の関係したときの保存則,熱力学の第1法則に到達した。電磁気の関与する現象ではさらに物体だけでなく場に蓄えられたエネルギーや光のエネルギーをも考慮することにより,つねにエネルギー保存則を成り立たせることに成功してきた。現在ではこの保存則は質量まで含めてつねに満たされるものと考えられている。いろいろな変化のうちに何か一定のものを求め,全宇宙でその総量が不変なものの存在を期待するのは,ギリシア時代以来人間の抱きつづけてきたほとんど哲学的な欲求であったといってよい。エネルギー概念の拡張と成功の歴史はエネルギーこそがまさにこの期待にこたえるものであることを示しつづけてきた。実際,仕事をする能力としての体系のエネルギーを,その状態で決まる状態量として保存則が満たされるよう定義し,その変換の法則を調べるということは,これまでの物理学の歴史における最大問題の一つであったということができる。この意味で,初め見かけ上の保存則のやぶれに対して,それを成り立たせるために導入され,のちに実際それが検証されたβ崩壊における中性微子(電荷0,静止質量0の粒子)の存在は,保存則が成功した非常に目ざましい例の一つということができよう。
執筆者:田辺 行人
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
化学辞典 第2版 「エネルギー」の解説
エネルギー
エネルギー
energy
エネルギーはしばしば“仕事をなしうる能力”(J.C. Maxwell,1879年)と定義される.F.W. Ostwald(オストワルト)(1910年)は“エネルギーは仕事そのもの,あるいは仕事からつくりだされるもの,または仕事に変換できるもの”と定義している.いずれにせよ,エネルギーは単に“能力”という以上に,適当な単位で測られ,適当な換算係数で互いに変換できる客観性のある物理量である.現在,エネルギーの基本単位として仕事の単位であるジュール(J)が用いられているのもこのことの反映であろう.エネルギーという語は,すでに18世紀後半,D'Alembertが編集に参画した百科大辞典中に見られ,かれはこのなかで静止する物体にはないが運動する物体がもつある種の“力”であるとした.T. Young(1807年)は,質量mの物体が速度vで運動するとき,mv2の積をエネルギーとよんだ.その後,W.J.M. Rankin(1853年)は,現在と同様の(1/2)mv2を“実エネルギー(actual energy)”とよび,またポテンシャルエネルギーという語を今日と同様の意味で用いた.W. Thomson(Lord Kelvin,1862年)は,今日と同様,(1/2)mv2を運動のエネルギー(kinetic energy)とよんだ.古い時代にはエネルギーはおもに機械的エネルギーだけが対象となっていたが,Thomsonはこれを熱力学の分野にも拡張し,固有エネルギー(intrinsic energy)の語を用いた(1878年).この語は比較的最近まで用いられていたが,現在ではもっぱら内部エネルギー(internal energy)とよばれているものである.エネルギーには種々の形態がある.上述の運動エネルギー,ポテンシャルエネルギー,熱エネルギー(内部エネルギー)のほか,放射線エネルギー,電気的エネルギー,磁気的エネルギー,化学エネルギー,表面エネルギー,原子核エネルギーなどがある.これらは,ある種の制約(たとえば,熱力学第二法則)はあるが,直接あるいは間接に仕事に変換することができ,また原子核エネルギーを除いては仕事からつくりだすことができる.[別用語参照]エネルギー保存則
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
百科事典マイペディア 「エネルギー」の意味・わかりやすい解説
エネルギー
→関連項目エネルギー革命|エルグ
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「エネルギー」の意味・わかりやすい解説
エネルギー
energy
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
栄養・生化学辞典 「エネルギー」の解説
エネルギー
世界大百科事典(旧版)内のエネルギーの言及
【エネルゲイア】より
…このように〈エネルゲイア〉概念はアリストテレス哲学の多くの重要な場面で大きな役割をになわされていた。また現代語〈エネルギー〉の語源でもある。【藤沢 令夫】。…
【力】より
…ルネサンス期の新プラトン主義に由来する錬金術的,占星術的,魔術的自然観は,デカルトを除く〈近代科学者〉といわれる人々にも多かれ少なかれ共有されたが,ケプラーからニュートンにいたる〈万有引力〉の着想の系譜もその伝統に属するし,さらに,ゲーテ以降のドイツ・ロマン主義や,自然哲学のなかに登場する〈力Kraft〉という概念も,同じ流れにある。この〈Kraft〉が,表現型としては多様であれ,自然の事物のなかにつねに一定に保たれる〈エネルギー〉という科学的概念の原型でもある。こうした考え方の最も徹底した形は〈力動説〉もしくは〈力本説〉(英語ではdynamism)と呼ばれる哲学上の主張になる。…
【動力】より
…機械的な仕事をさせるのに直接利用できるエネルギー,もしくはその働きをいう。英語のpowerの訳語と考えられ,一般に,機械を動かすエネルギー(動力源がもたらす発生動力),その機械によって消費されるエネルギー(消費動力,吸収動力)およびそのエネルギーが機械的な形で伝えられること(動力伝達)に対して動力ということばを使うことが多い。…
【有用植物】より
…そのようなものから栽培化されたものにアフリカ原産のアブラヤシがあり,熱帯域では最も生産性の高い油料植物となっている。単位面積あたりの生産性の高い油料植物の育成は,油脂が食料にとどまらず,エネルギー源としても重要な位置を占めるようになるだろうから,努力をはらわねばならない。工芸作物
[糖源植物]
植物体は,成分的には多糖類である高分子化合物のセルロースを骨格に形成され,やはり多糖類であるデンプンが貯蔵物質となっていることが多い。…
※「エネルギー」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...