ベルヌーイ数（読み）ベルヌーイすう（英語表記）Bernoulli number

改訂新版　世界大百科事典

ベルヌーイ数 (ベルヌーイすう)
Bernoulli number

x/（e^x－1）の原点におけるテーラー展開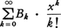の係数B_kをベルヌーイ数と呼ぶ。B₀＝0，B₁＝－1/2，B_2l+1＝0（l≧1）である。またB_2lはlが奇数のとき正，lが偶数のとき負である。B₂＝1/6，B₄＝－1/30，B₆＝1/42，B₈＝－1/30，B₁₀＝5/66，B₁₂＝－691/2730であり，ベルヌーイ数はすべて有理数である。ベルヌーイ数は数論やトポロジーなど数学の種々の分野に登場する。ヤコプ・ベルヌーイは確率の研究中に公式，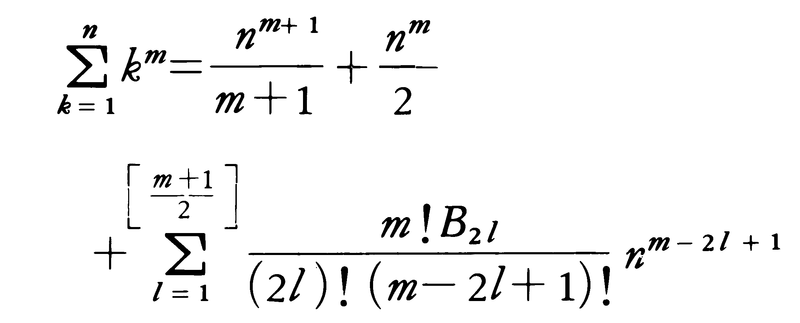

を見いだした。ここで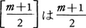をこえない最大の整数を表す。このことによってB_2lはベルヌーイ数と呼ばれる。B_2lをB_lと書くことや（－1）^l⁺¹B_2lをB_2lと書くこともある。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

ベルヌーイ数
ベルヌーイすう
Bernoulli number

自然数のべきの和を求める多項式 (ベルヌーイの多項式) の展開に伴って見出される有理数で，J.ベルヌーイ (1世) にちなんでこう呼ばれる。 x/(e^x－1) をべき級数に展開し，x/(e^x－1)＝ΣB'_n(xⁿ/n!)＝B'₀＋B'₁(x/1!)＋B'₂(x²/2!)＋… としたときの係数として現れ，B'₀＝1，B'₁＝－1/2，B'₂＝1/6，B'₃＝0，B'₄＝－1/30，B'₅＝0，B'₆＝1/42，… である。しかし，一般に応用数学の分野では，ベルヌーイ数を B_n とすると，B_n＝(－1)^n-1B'_2n とおいて，B_n＝2(2n)!ζ(2n)/(2π)²ⁿ ( ζ はゼータ関数) で表わされ，B₁＝1/6，B₂＝1/30，B₃＝1/42，B₄＝1/30，B₅＝5/66，… とされる。すなわち符号因子 (－1)ⁿ をつけることによってすべてを正の有理数にするのである。これらの数をベルヌーイ数という。

出典　ブリタニカ国際大百科事典 小項目事典