トポロジー（読み）とぽろじー（英語表記）topology

デジタル大辞泉

トポロジー（topology）

１ 位相。また、位相幾何学、位相数学。トポロギー。
２ ⇒ネットワークトポロジー

出典　小学館

精選版 日本国語大辞典

トポロジー

1. 〘 名詞 〙 ( [英語] topology )
2. ① 幾何学の一部門。図形の性質のうち、位相写像（それ自身も逆写像も連続であるような全単射）によって不変に保たれるものを研究対象とするもの。位相数学。
3. ② 図形や空間のもつ位相数学的性質。位相。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

トポロジー
とぽろじー
topology

図形すなわち一般には位相空間の位相的に不変な性質や概念を研究する幾何学がトポロジーであり、オイラーやガウスにその研究の萌芽(ほうが)をみることもできるが、本格的には、20世紀初頭よりフランスの数学者・物理学者ポアンカレによって創始された現代数学の一つの分野である。トポロジーは、位相空間論、組合せトポロジー、代数的トポロジー、微分トポロジーに大別される。トポロジーはまた位相幾何学ともよばれるが、この場合は位相空間論を含まないのが普通である。

　XとYとが位相空間であるとき、XよりYの上への一対一写像f:X→Yがあり、fおよびその逆写像f^-1:Y→Xとがともに連続であるとき、XとYとは同位相であるといい、fを同位相写像homeomorphismという。同位相な位相空間が共通にもつ性質や概念（たとえば基本群、ホモロジー群、ホモトピー群など）は位相的に不変であるという。曲面でいえば、球面と楕円(だえん)面とは、それらが理想的なゴム膜からできているとするとき、破ったり貼(は)ったりしないで互いに変形できるので同位相である。すなわち、理想的なゴム膜の切り貼りしない自然な変形は、同位相写像とみなせる。

　ポアンカレ以来、彼が提出したポアンカレの予想をめぐって、まず組合せトポロジーおよび代数的トポロジーが発展し、第二次世界大戦ころより微分トポロジーが台頭し、ポアンカレ予想の一部分を解決するなどの大発展をなし、カタストロフィー理論や力学系の理論へとその研究が拡大されるとともに、現代数学での基礎理論となり、各分野で応用されている。

［野口　廣］

組合せトポロジー

オイラーが18世紀に考えたケーニヒスベルクの橋の問題やオイラーの多面体の公式などが組合せトポロジーの誕生を告げるものである。組合せトポロジーでは、点と線分と三角形と四面体、一般にn次元単体に三角形分割できるような位相空間、すなわち多面体を考え、この位相的性質をこれら単体間の結合の仕方として代数的に表現する。

［野口　廣］

基本群

ポアンカレはホモロジーに続いて基本群を考えた。これは多面体（一般に位相空間でよい）Xのある頂点x₀を固定し、単位円周S¹の一点Oがこのx₀に写るようにS¹をXへ写す連続写像f:S¹→Xの集合を考える。この集合の元fとgとは、パラメーターtをもつこうした写像の族
　　｛f_t｜0≦t≦1｝ただし f₀=f, f₁=g
が存在するとき、互いにホモトピックであるという。このホモトピックの考えで写像の集合を分類した同値類は、それが含む写像がfであれば［f］で示すことにする。これら同値類［f］,［g］は、fとgとの結合を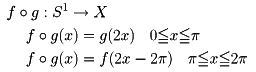

と定めて、［f］と［g］の積を［f゜g］と定めると、この同値類の集合は群をなし、これをXの基本群π₁(X)とよぶ。たとえば、円周S¹、球面S²、三次元球面S³、一般にn次元球面Sⁿの基本群は、
　　π₁(S¹)=Z　整数の加群
　　π₁(S²)=0　単位元のみ
　　π₁(S³)=π₁(Sⁿ)=0
　　　　　　　　単位元のみ　n≧4
であり、トーラスTの基本群は
　　π₁(T²)=Z+Z　（整数の加群2個の直積）
である。

［野口　廣］

ポアンカレの予想

ポアンカレの予想とは、三次元球面とホモロジー群も基本群も同じである三次元閉多様体は、三次元球面に限るという主張である。類似の予想が一般のn次元でも考えられる。すなわち、n次元球面と同じホモロジー群や同じホモトピー群をもつn次元閉多様体はn次元球面である。これを一般次元のポアンカレの予想という。

［野口　廣］

代数的トポロジー

基本群の考えは、1935年にフレビッチWitold Hurewicz（1904―1956）によってホモトピー群へ拡張され、ホモロジー群と相まって位相空間の位相的性質が群論的に研究され始めた。これは代数的トポロジーの発展であり、コホモロジー群なども研究され、1950年代にはホモロジー論は公理化された。その後一般コホモロジー論はK理論やホモロジー代数へと発展している。

［野口　廣］

最近の発展――微分トポロジー

ポアンカレは天体力学の軌道の問題からトポロジーの研究を志したから、本来微分学とトポロジーとは深く関連すべきものであったが、ポアンカレはその基本的研究として前記の組合せ、代数的トポロジーをまず展開した。1936年ころより微分多様体の概念がホイットニーHassler Whitney（1907―1989）により確立され、彼によって基本的理論が準備された。1940年代にケアンズSteward Scott Cairns（1904―1982）およびホワイトヘッドが、微分多様体は三角形分割できること、すなわち多面体である（組合せ多様体となる）ことを示した。そして第二次大戦後ファイバー・バンドル（ファイバー束）の理論が整備され、代数的トポロジーの成果を背景として微分トポロジーは1950年代に爆発的に発展した。すなわち、1954年にトムR. Thomは、二つのn次元閉多様体M₁とM₂は、あるn+一次元多様体Nの境界∂N=M₁-M₂になるとき同境であると定めて、ホモトピー理論を用いて多様体を分類した。この結果は多様体を位相的に分類するというトポロジー究極の目標へ向けての貴重な一歩であり、今日コボルディズム理論とよばれている。

　1956年にはミルナーJohn Willard Milnor（1931―　）は、七次元球面S⁷と同位相ではあるが、S⁷のような微分構造をもたない微分多様体を発見し、これらをエキゾティックな球面と命名した。ミルナーは組合せトポロジーを深めたPLトポロジーを展開し、PL多様体の微分構造、とくにエキゾティックな高次元球面の詳しい研究を進めた。1962年にスメールStephen Smale（1930―　）は、n≧5の場合のポアンカレ予想を肯定的に解決した。

　ポアンカレの予想と並んで、トポロジーの基本的問題として基本予想がある。これは、組合せ多様体が二つの三角形分割K₁、K₂をもつとき、それらは組合せ的に同じ分割であるか否かという問題である。そしてさらに、そもそも多様体は三角形分割できるものかどうかという三角形分割の問題も同様に重要な問題であり、また、多様体に微分構造がいつも入るのか否かという問題もある。これらの問題は組合せトポロジー、代数的トポロジー、そしてPLトポロジーや微分トポロジーにわたる難問であったが、シーベマンL. C. Siebenmann（1939―　）が1969年に基本予想の反例をつくり、また三角形分割できない多様体のあることや、さらに微分構造をもたない多様体の存在も知られるに至っている。そして1982年にn=4の場合のポアンカレ予想が、フリードマンM. H. Freedmanによって解かれた。

［野口　廣］

『本間竜雄著『新しいトポロジー』（講談社・ブルーバックス）』

[参照項目] | 微分トポロジー | ホモロジー

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

トポロジー
topology

(1) 位相数学，位相幾何学ともいう。位相数学は初め，幾何学的図形の連結性の研究を目的として生れたが，20世紀に入り，近さ，極限の考えを一般化した位相の概念が確立された。それにより幾何学的図形以外の対象にも適用されるようになり，数学の諸分科ばかりでなく，数理科学の諸分野から，心理学や社会科学の分野にも寄与している。 (2) 近さの考えを一般化した概念で位相と訳す。ある集合に位相を定義するには，その集合に，適当な構造を与えて，連続性あるいは極限の概念が定義できるようにすればよい。集合 S に対し位相を導入する具体的な方法としては，S の各部分集合 M に対しその極限点の全体を指定すれば十分である。古典的な型の幾何学における空間には，すべて極限点が定義できるから，これらはすべて位相空間となる。しかし，一般の空間に位相を導入するのによく行われるのは，開集合を指定する方法である。集合 E ( ≠φ ) の部分集合の集合 T が次の3条件を満足するとき，T は E の位相構造 (位相) を定めるという。 (a) E 自身および空集合は，T に属する。 (b) A および B が T に属すれば，A と B の共通部分も T に属する。 (c) T に属する任意個 (有限または無限個) の集合の合併集合もまた T に属する。このようにして位相の定められた集合 E を位相空間，E の元を点，T に属する個々の集合 ( E の部分集合) を E の開集合という。 (3) 現在の位相数学は，一般に，位相空間における集合論的，代数学的，解析学的な研究に関する数学の一分野である。ただし，慣習的に位相幾何学というときには，幾何学的ないし代数学的色彩を伴った対象，特に多様体に関する研究をそう呼ぶことが多い。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

トポロジー
topology

集合上に〈近さ〉とか〈近づく〉といった概念で表される構造が与えられると，その集合上で極限や連続について論ずることができるが，このような構造をトポロジー（訳して位相）と呼ぶ。また，この構造が内容や方法上で問題となる数学のことを広くトポロジー（訳して位相数学）と呼ぶこともあるが，ふつうはもっと狭く，図形の位置や形状に関する性質で，図形を構成する点の連続性にのみ依存するものを研究の対象とする数学のことをトポロジー（訳して位相幾何学）と呼ぶ。リスティングJ.B.Listingは1847年に著書《Vorstudien zur Topologie》を出版し，トポロジーということばを使っているが，この数学の実質的創始者であるH.ポアンカレは，この数学をanalysis situs（位置解析学）と呼び，長らくこのことばが使われていた。トポロジーということばが普及したのはS.レフシェッツの著書《Topology》（1930）の影響が大きい。
→位相幾何学
執筆者：中岡 稔

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

トポロジー

広義では位相数学。狭義では位相幾何学。

出典　株式会社平凡社

ASCII.jpデジタル用語辞典

トポロジー

元々は位相幾何学の意味であるが、パソコン用語としては、LANの接続形態の総称。ネットワークトポロジーとも呼ばれる。LANには接続形態によって、リング型やバス型、スター型などがあり、接続する機器によって用途や目的に合った接続形態を使用する必要がある。

出典　ASCII.jpデジタル用語辞典

世界大百科事典（旧版）内のトポロジーの言及

【位相】より

…(1)数学用語。トポロジーtopologyともいう。数学において極限や連続の概念は中心的役割を演ずるが，これらの概念は実数の集合や平面上の点集合については“近さ”とか“近づく”といった概念を用いて定義される。…

【位相幾何学】より

…トポロジーともいう。図形を構成する点の連続的位置関係のみに着目する幾何学。…

【幾何学】より

…そこで，同相写像によって変わらないような性質を研究する幾何学というものが考えられる。トポロジーtopologyはこのような研究を主目的とする数学であって，位相幾何学と訳されているように，この幾何学では図形の位置や形相に関した性質で，点の連続性にのみ依存する性質が扱われる。位相幾何学は位置解析学analysis situsという名称でG.W.ライプニッツによって予見されていたが，具体的な業績はオイラーによって初めて与えられた。…

※「トポロジー」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」