ランジュバン方程式 (ランジュバンほうていしき)
Langevin equation
水中の微粒子は,水の分子と衝突して不規則な運動をしているが,水平方向の速度U(t)は次の方程式に従い変動する。aを摩擦係数,B(t)をブラウン運動とすると,
dU(t)=-aU(t)dt+λdB(t)
この方程式は,ランダムな外力が加えられたときの運動を記述するのに,P.ランジュバンが用いた方程式と類似するため,ランジュバン方程式と呼ばれている。ランジュバン方程式は線形な確率微分方程式で,定常解は,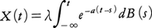 と確率積分で表され,オルンシュタイン=ウーレンベックOrnstein-Uhlenbeckのブラウン運動と呼ばれる正規定常なマルコフ過程である。
と確率積分で表され,オルンシュタイン=ウーレンベックOrnstein-Uhlenbeckのブラウン運動と呼ばれる正規定常なマルコフ過程である。
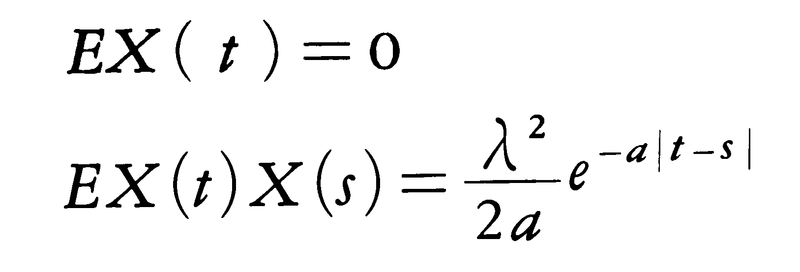
となり,エルゴード性をもつ。統計力学の〈ゆらぎ〉の解析に用いられるなど,物理現象の記述に利用されているが,最近,コンピューターの発達と観測の精密化により,実際の現象と合わないことが多くなり,遅れのあるランジュバン方程式など,一般化が試みられ,成果をあげている。
執筆者:西尾 真喜子
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ランジュバン方程式
ランジュバンほうていしき
Langevin equation
ブラウン運動を記述する確率的な運動方程式。粒子の速度を v,質量を m,抵抗係数をγとすると,次の式で与えられる。
m(dv/dt)=-γv+F(t)
F(t) は粒子が受ける力から,平均の抵抗力 -γv を除いたもので,揺動力と呼ばれる。この方程式は確率的に変化する力 F(t) によって駆動されるブラウン粒子の速度 v(t) を定める。 F(t) の最も簡単な場合は,〈F(t)〉=0,〈F(t)F(t')〉=2γkTδ(t-t') である。〈 〉は時間平均,kはボルツマン定数,Tは絶対温度,δはδ関数である。また速度 v(t) の確率分布はこの方程式に等価なフォッカー=プランク方程式に従い,十分に長い時間が経過したのちの粒子の変位 xに対しては,アインシュタインの拡散式 〈x2〉=2(kT/γ)t が成り立つ。この方程式は流体中のブラウン運動ばかりでなく,固体中の電子やスピン運動の研究に対しても応用されている。森肇はこの方程式を数学的に厳密に導くことに成功した。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内のランジュバン方程式の言及
【ブラウン運動】より
…ポーランドのM.vonスモルコフスキー,ドイツのフォッカーAdriaan Daniël FokkerおよびM.プランク,フランスのP.ランジュバンによって発展され,さらにのちにはN.ウィーナーにより確率過程の数学の一部門にもなっていく。フォッカー=プランクの方程式は微粒子の位置と速度の確率分布関数がみたすべき方程式であり,[ランジュバン方程式]は微粒子の運動方程式で,速度の減衰項や外力(重力)のほかに,ランダム・ノイズとしてのゆらぐ力を含んでいる。分子衝突に起因するゆらぎの力は確率変数である。…
※「ランジュバン方程式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
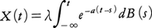 と確率積分で表され,オルンシュタイン=ウーレンベックOrnstein-Uhlenbeckのブラウン運動と呼ばれる正規定常なマルコフ過程である。
と確率積分で表され,オルンシュタイン=ウーレンベックOrnstein-Uhlenbeckのブラウン運動と呼ばれる正規定常なマルコフ過程である。