ゆらぎ
fluctuation
物理量が平均値を中心として変動する現象。揺動ともいう。ある体系の物理量を観測する場合、実際の測定値はその平均値で、物理量そのものの値は時々刻々あるいは場所によって変動している。このような変動がゆらぎである。
たとえば、適当な容器に気体を封入したとして、その圧力を考える。この気体は、微視的にみれば、莫大(ばくだい)な数の分子から構成されている。これらの分子は容器中で乱雑な分子運動を行うが、分子が壁に衝突すると壁により跳ね返され、その際に分子は壁に力を及ぼす。力学の作用・反作用の法則により、逆に壁は気体を押す向きに力を及ぼす。このような力を気体分子全体に対して加え、それを単位面積当りに換算したものが気体の巨視的な圧力である。ところで、壁のある箇所(図の灰色の部分)に注目し、そこでの圧力を時間的に追跡したとする。衝突する分子が多かったり、少なかったり、またその速さや方向が不規則なため、圧力は時間の関数として一定ではなく図のように平均値Pの周りで変動する。この種の変動がゆらぎである。
統計力学では、注目する体系の集団(アンサンブル)を考え、そこでの物理量の確率分布を考察する。それらの集団での個々の系での平均からのずれがゆらぎである。アンサンブルでの平均を〈 〉の記号で表すことにすると、物理量Aの平均は〈A〉であり、その分散はσ2=〈(A-〈A〉)2〉である。このときの平均からのずれはσで表される。σ2は系の大きさNに比例する量であるので平均からのずれσは熱力学極限では平均自身に比べて無視できるようになる。また、一般にAに共役な外場aに対する応答
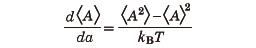
で与えられる。ここで、Tは温度、またkBはボルツマン定数である。このように、ゆらぎ〈A2〉-〈A〉2と応答d〈A〉/daの間に比例関係が成り立つ。この関係はカークウッドKirkwoodの関係とよばれ、広い意味での揺動散逸定理の例になっている。また、比熱Cは共役な外場の温度であるため、表式は少し変わるがやはりエネルギーEのゆらぎで与えられる。

上でみたように通常の状態では、巨視的体系の平均からのずれは小さいが、臨界点近傍ではゆらぎが異常に大きくなる。この場合は応答も発散する。そのため、二種類の液体の混合状態の臨界点近傍では、密度のゆらぎも大きくなり、その大きさが光の波長と同程度になるとき強く散乱が起き、その結果、系はミルク状にみえる。この現象を臨界タンパク光という。
磁性体でも強磁性から常磁性へと転移する温度(キュリー点という)の近くで、磁化のゆらぎが異常に大きくなり、キュリー点に近づくと、磁化率は無限大となる。
[阿部龍蔵・宮下精二]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
ゆらぎ
fluctuation
一般に平均量からの個々の値のずれ,または平均値の近くで変動する現象全体をゆらぎという。揺動ともいう。例えば,容器に入っている気体を考えると,その密度は平衡状態では通常どこでもいつも一定とみなされる。気体の性質,例えばボイル=シャルルの法則を議論するにはそれで十分である。しかし,密度とは一小部分に含まれる物質の質量とその体積の比で定義され,気体は多くの分子からできていて,それが激しく運動しているから,同一の温度と圧力の下でも,微小な同体積中にいつも同数の分子が存在するとは限らない。すなわち,密度は時間的に変動している。また,微小部分の位置によっても密度は変動している。通常密度と呼んでいる量はその平均にほかならない。この例のように,物質の熱力学的量はミクロな量,すなわち分子的な量の平均で与えられ,その平均のまわりには必ず変動がある。これがゆらぎである。
ゆらぎの大きさを表すものとして,分散σがある。いまある量Aの平均値をA-で表すことにする。変動量をxとし,その平均をxとすると,分散σは,
 で定義される。分散σが大きいほどゆらぎは大きい。ゆらぎの種類にはいろいろあって,その大きさを表す分散だけではゆらぎの特徴を記述することはできず,ゆらぎ⊿x≡x-xの分布関数,または時間的なゆらぎ⊿x(t)に対してはそのスペクトル分布が重要である。もっとも典型的なゆらぎは,ガウス的なゆらぎで,その分布関数P(⊿x,t)は,
で定義される。分散σが大きいほどゆらぎは大きい。ゆらぎの種類にはいろいろあって,その大きさを表す分散だけではゆらぎの特徴を記述することはできず,ゆらぎ⊿x≡x-xの分布関数,または時間的なゆらぎ⊿x(t)に対してはそのスペクトル分布が重要である。もっとも典型的なゆらぎは,ガウス的なゆらぎで,その分布関数P(⊿x,t)は, で与えられる。したがって,この分布は分散σだけで特徴づけられる。もう一つの有名な例はポアソン分布で,変動量を正または0の整数n(=0,1,2,……)としたとき,平均m≡nだけで特徴づけられ,その分布は,
で与えられる。したがって,この分布は分散σだけで特徴づけられる。もう一つの有名な例はポアソン分布で,変動量を正または0の整数n(=0,1,2,……)としたとき,平均m≡nだけで特徴づけられ,その分布は,
P(n)=mne⁻m/n!
で与えられる。これは,ごくまれにぽつんぽつんと起こる現象,例えば単位時間に観測される放射線の粒子の数などによく適用できる分布である。前者のガウス分布は,小さな独立の変動の集合として観測される量によくあてはまる分布で,測定誤差などは,ガウス分布に従う典型的なゆらぎの例である。
ゆらぎは,二つの意味でたいへん重要な概念である。第1は,電気伝導,熱伝導,粘性などの非平衡系の輸送係数が,平衡系でのゆらぎで記述されるからである。これは揺動散逸定理と呼ばれ,非平衡統計力学におけるもっとも基本的な定理である。また,平衡系に時間によらない外場を加えたときの応答,例えば磁化率は磁化のゆらぎで表され,比熱はエネルギーのゆらぎで表される。第2は,巨視的な秩序形成において,時間の初期領域で,ゆらぎは決定的に重要な役割を果たしている。すなわち,無秩序状態においてゆらぎとして現れた小さな秩序変数が,体系の非線形性によって,どんどん大きく成長し,やがて巨視的な量にまで発展するのである。これが巨視的秩序形成のメカニズムである。
二次相転移が起こるときには,比熱などの物理量のゆらぎが異常に大きくなる。多くの場合,それは臨界点で発散する。逆に,ゆらぎの発散によって,相転移点を観測することができる。
→臨界現象
執筆者:鈴木 増雄
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
ゆらぎ
ユラギ
fluctuation
一般に,ある量がその平均値のまわりに変動する現象をゆらぎという.ある量Xの出現確率をP(X)とすれば,その平均値は,
 =
=  XP(X)
XP(X)
で定義される.ただし,和はXのとりうるすべての値について行うものとする.さらに,平均値からのずれ方の程度を示す分散
σ 2 = 
 P(X)
P(X)
が導入される.分散の平方根σ(標準偏差)を物理学ではゆらぎとよぶ.体系がたとえ熱平衡状態にあっても,微視的にみればいろいろの量がゆらぎの現象を示している.巨視的な測定によって確定した値が得られるのは,ゆらぎが小さくて無視できるからである.たとえば,温度Tで熱平衡状態にある古典理想気体中での粒子密度
N/V = ρ
のゆらぎは,

で与えられる.
 ≅ 1023 mol-1
≅ 1023 mol-1
であるから,このゆらぎはきわめて小さいものである.観測の精度や観測しようとする量によっては平均値からのずれをとらえることができ,それからその体系の微視的構造についての知識を引き出すことができる.とくに,体系の時間的変化の問題に対してのゆらぎの現象が重要な意味をもっている.[別用語参照]ブラウン運動
出典 森北出版「化学辞典(第2版)」化学辞典 第2版について 情報
Sponserd by 
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
ゆらぎ
揺動とも。一般に平均量からの個々の値のずれ,または平均値の近くで変動する現象全体。たとえば容器内の気体の圧力は,気体分子の容器壁に及ぼす力の平均値を示しているが,気体分子は激しく振動しているので瞬間の圧力を細かに測定すれば,平均の圧力を中心にしてゆらいでいる。このゆらぎが測定されないのは分子数が非常に多いからである。
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
世界大百科事典(旧版)内のゆらぎの言及
【加法過程】より
…このように増分が過去と独立になるような確率過程を加法過程,または独立増分過程と呼ぶ。連続時間をもつ確率過程X(t)についても同様にして,時刻tから後の時刻t+h(h>0)までの変移X(t+h)-X(t)がt以前の値{X(s);s≦t}と独立になるものを加法過程と呼び,応用面では,理想的なゆらぎやノイズなどの数学的記述と考えられている。とくにX(t+h)-X(t)の分布がtに無関係なとき時間的に一様であるという。…
※「ゆらぎ」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
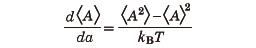





 で定義される。分散σが大きいほどゆらぎは大きい。ゆらぎの種類にはいろいろあって,その大きさを表す分散だけではゆらぎの特徴を記述することはできず,ゆらぎ⊿x≡x-
で定義される。分散σが大きいほどゆらぎは大きい。ゆらぎの種類にはいろいろあって,その大きさを表す分散だけではゆらぎの特徴を記述することはできず,ゆらぎ⊿x≡x- で与えられる。したがって,この分布は分散σだけで特徴づけられる。もう一つの有名な例は
で与えられる。したがって,この分布は分散σだけで特徴づけられる。もう一つの有名な例は =
=  XP(X)
XP(X)
 P(X)
P(X)
 ≅ 1023 mol-1
≅ 1023 mol-1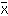 のまわりに値が変動すること,またはその変動の大きさ。数学的には(x-
のまわりに値が変動すること,またはその変動の大きさ。数学的には(x-