中間値の定理（読み）ちゅうかんちのていり（英語表記）intermediate-value theorem

改訂新版　世界大百科事典

中間値の定理 (ちゅうかんちのていり)
intermediate-value theorem

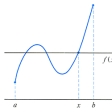
閉区間［a，b］で連続な実数値関数f（x）があって，f（a）≠f（b）ならば，f（a）とf（b）との間の任意の実数αに対して，f（c）＝αとなるcがaとbの間に存在する。この事実を中間値の定理という。このことは次のようにしてわかる。例えばf（a）＜f（b）とすると，xy平面上の点A（a，f（a））は直線y＝αより下にあり，点B（b，f（b））は直線y＝αより上にあって，関数y＝f（x）のグラフはAからBに至る連続曲線であるから，そのグラフはa＜x＜bの範囲で直線y＝αと少なくとも1回交わる。その一つの交点のx座標をcとすればf（c）＝αとなる。

　中間値の定理は多変数の場合も成り立つ。平面，空間，一般にn次元空間の中の連結集合Eで連続な実数値関数f（P）があって，Eの2点P₁，P₂に対してf（₁）≠f（P₂）ならば，f（P₁）とf（P₂）との間の任意の実数αに対して，f（P₃）＝αとなる点P₃∈Eが少なくとも一つ存在する。
執筆者：伊藤 清三

図－中間値の定理

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

中間値の定理
ちゅうかんちのていり
intermediate value theorem

連続関数 f について，f(a) と f(b) の間の任意の中間の値を [a，b] でとる，という定理。実数の連続性として，区間が連結集合であることを根拠にしている。これは，連続関数ではグラフがつながっていることを意味している。しかし，連続関数というのは連結性とは別の概念で，グラフがつながっている関数が連続関数であるとは，一般にはいえない。 f が微分可能のとき，導関数 f' は連続とはかぎらないが，中間値の定理は成立する。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

中間値の定理
ちゅうかんちのていり

閉区間［a,b］において連続な関数f(x)は、x=aにおいてとる値と、x=bにおいてとる値の中間のすべての値を区間［a,b］のなかでとる、という定理である。この定理は、一見きわめて当然のことを述べているようであるが、これは実数の本質と深いかかわりがあり、実数の基本的性質の一つ、といってよい意味があるのである。一方、この定理の利用される場は、非常に大きい。

［竹之内脩］

中間値の定理

出典　小学館　日本大百科全書(ニッポニカ)