凸関数（読み）とつかんすう（英語表記）convex function

精選版 日本国語大辞典

とつ‐かんすう‥クヮンスウ【凸関数】

1. 〘 名詞 〙 数学で、関数の一つ。そのグラフと、それより上の部分との和集合が凸集合であるような関数をいう。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

凸関数 (とつかんすう)
convex function

一つの区間で定義されている実数値関数f（x）が，この区間の任意の2点x₁，x₂に対して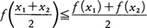，を満たすときこれを凸関数という。区間a≦x≦bにおいてf（x）が凸関数であって，その一つの部分区間で上に有界ならば，f（x）は区間a＜x＜bで連続である。f（x）が連続である区間においては，f（x）が凸関数であることは，y＝f（x）のグラフが“下に凸”であることと同じである（図）。a＜x＜bで2回微分可能な関数f（x）が，そこで凸関数であることは，f″（x）≧0なることと同等である。例えばx^p（p＜0またはp＞1），－x^p（0＜p＜1），－log x，xlog xは0＜x＜∞において凸関数であり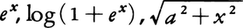，は－∞＜x＜∞において凸関数である。凸関数は種々の不等式を導くのにも用いられる。f（x）がa≦x≦bで連続な凸関数ならば，その区間に属する任意のx₁，……，x_nと任意の正数α₁，……，α_nに対して，不等式，

が成立する。例えばa_ν＞0，b_ν＞0（ν＝1，……，n），p＞1，1/p＋1/q＝1（したがってq＞1）のとき，上の不等式でf（x）＝x^q，α_ν＝a_ν^p，x_v＝b_v/a_v^p/qとすると，ヘルダーO.Hölderの不等式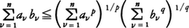，を得る。
執筆者：伊藤 清三

図－凸関数

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

凸関数
とつかんすう
convex function

関数 y＝f(x) の定義されている区間内で，3点 x₁ ，x₂ ，x₃ が x₁＜x₂＜x₃ のようにとられているとき，これらの3点に対して，
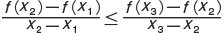が成り立てば，f(x) は凸関数と呼ばれる。 x₁ ，x₂ ，x₃ に対応する曲線上の点を P₁ ，P₂ ，P₃ とすれば上の不等式の左辺は線分 P₁P₂ の傾きを示し，右辺は線分 P₂P₃ の傾きを示しており，しかも上の不等式全体は，P₁P₂ の傾きが P₂P₃ の傾きよりも大きくないことを示している。もっと簡単には，関数 y＝f(x) のグラフ上の2点 P₁ ，P₂ を結んだ線分 P₁P₂ が，それら2点間にあるグラフよりも上にあれば，関数 f(x) は凸関数であるといってもよい。この定義では，1次関数も凸関数になってしまうが，この不等式が ≦ でなくて ＜ になったときは，狭義の凸関数または真に凸な関数という。

出典　ブリタニカ国際大百科事典 小項目事典