凸集合（読み）とつしゅうごう

精選版 日本国語大辞典

とつ‐しゅうごう ‥シフガフ【凸集合】

〘名〙 平面や空間の部分集合の一つ。平面や空間の部分集合で、その二点を結ぶいかなる線分もまたそれに含まれるものをいう。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

凸集合
とつしゅうごう

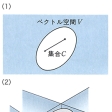
実数を係数にもつベクトル空間Vの中の集合Cで、その中の任意の2点を結ぶ線分上のすべての点が、またCに属するようなものを凸集合という（図の(1)）。Vの二つの要素v、wに対して、それを結ぶ線分上の点xは、適当なα(0＜α＜1)を用いて、
　　x=αv+(1-α)w
と表される（Vがアフィン空間であるとき、
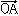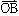　　v=,w=,x=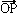
とすれば、Pは線分ABを(1-α):αに内分する点を表している）。したがって、Cが凸集合である条件は、
　　v,w∈C, 0＜α＜1　ならばつねに
　　αv+(1-α)w∈C
と述べることができる。二次元平面内における有界な凸集合（一直線上にはのらないものとする）の境界の曲線は卵形線、また三次元空間内の有界凸集合の境界面は卵形面とよばれ、幾何学的考察の対象となっている。凸集合は、半空間の共通部分として表される（図の(2)）。区間［a,b］で定義された関数f(x)は、そのグラフより上側の点全体の集合が凸集合となるとき（図の(3)）、すなわち、集合
　　｛(x,y)|a≦x≦b,y≧f(x)｝
が凸集合となるとき、下に凸という。あるいは単に凸関数という。滑らかな関数の凸の状態はその二階の導関数の符号を調べて判定することができる。数学に現れる不等式の多くが、凸集合、凸関数と密接に関連している。

［竹之内脩］

凸集合説明図〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

凸集合 (とつしゅうごう)
convex set

ユークリッド空間の部分集合Aであって，Aのどんな2点をとってもそれらを結ぶ線分はAに含まれるという性質を満たすものを凸集合という。例えば，円板や球体，またはそれらの内部は凸集合であるが，円周や球面は凸集合ではない。いくつかの凸集合の共通部分はまた凸集合である。ユークリッド空間の任意の部分集合Xに対し，Xを含む最小の凸集合をXの凸包といい，とくに有限個の点からなる集合の凸包を凸胞体という。例えば線分はその端点，三角形や四面体はそれらの頂点の作る集合の凸包で，したがって凸胞体である。
執筆者：中岡 稔

図－凸集合

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

凸集合
とつしゅうごう
convexity; convex set

平面上に有界な点集合 S があるとき，S の任意の2点P，Qに対して，PとQを結ぶ線分がまた S に含まれるとき，S は凸あるいは凸集合であるという。一般にベクトル空間の点集合についても同様にして凸集合を定義する。たとえば，平面上の円や楕円や三角形の内部は凸集合であり，普通の空間では，球などが凸集合である。一般に空集合は凸集合と考える。凸集合の周になっている線を凸閉曲線という。

出典　ブリタニカ国際大百科事典 小項目事典