リウビル
りうびる
Joseph Liouville
(1809―1882)
フランスの数学者。サン・オメールの生まれ。1831年より理工科大学校(エコール・ポリテクニク)の、1851年から1879年まではコレージュ・ド・フランスの教授を務めた。1839年以降は科学アカデミー会員。関数論において、「複素数平面全体で有界正則な関数は定数である」「周期平行四辺形内に極をもたない楕円(だえん)関数は定数である」などを示した。また微分方程式
y(n)+p1(x)y(n-1)+……+pn(x)y=0
のn個の解y1,y2,……,ynについて、ロンスキーH. Wronski(1776―1853)の行列式
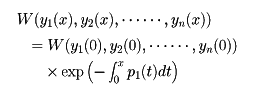
の成り立つことを示した。なおまた、「リッカチJ. Riccati(1676―1754)型微分方程式
y'+p1(x)y2+p2(x)y+p3(x)=0
は一般には求積法では解けない」ことを示し(1841)、さらに弦の振動数λを求める「スチュルム‐リウビル微分方程式の解によって一般関数を展開する問題」の研究や、係数が整数であるn次代数方程式の解にならない「超越数」の研究も有名である。なお、夭逝(ようせい)したガロアの遺稿を1846年に整理して発表したことは、リウビルの功績として後世に名をとどめるものである。
[吉田耕作]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
リウビル
Joseph Liouville
生没年:1809-82
フランスの数学者。1825年エコール・ポリテクニクに入学,2年後に橋梁(きようりよう)土木学校に移ったが,数学や数理物理学の研究を続けた。1828-30年にかけて論文を七つ書いてアカデミー・デ・シアンスに送り受理され,31年エコール・ポリテクニクの教師となり,38年教授に昇進,翌年アカデミー・デ・シアンス会員に選出された。51年にはコレージュ・ド・フランスの教授となる。彼の業績は,ほぼ数学全般にわたっており,約400編の論文を発表したほか,36年に雑誌《純粋応用数学誌(リウビル誌)》を創刊し,74年までその編集に打ち込んだ。彼の論文のなかには超越数の存在証明,任意位数の微分と積分およびハミルトンの正準方程式の解は時間の進行に対して位相空間の測度を保存するなど後来の研究に影響を及ぼしたものが多い。たとえば正準方程式に関する保存定理は,統計力学におけるエルゴード理論の基礎になった。なおリウビルが,早熟の天才E.ガロアの残した諸論文を理解しようと努力し,その中でもっとも重要な代数方程式がべき根によって解かれる諸条件を明らかにしたものなどを前述の雑誌に発表したことは,数学者リウビルの名誉として永く語り継がれるであろう。
執筆者:吉田 耕作
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
リウビル
フランスの数学者。エコール・ノルマル,コレージュ・ド・フランス,パリ大学各教授を歴任。1836年《純粋・応用数学雑誌》(別名リウビル誌)を創刊,これにガロアの業績を紹介。微分方程式,超越数,関数論等を研究。
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
世界大百科事典(旧版)内のリウビルの言及
【超越数】より
…彼は1748年ころ自然対数の底e,円周率πなどは超越数であろうと予想したが,eが無理数であることしか証明できなかった。1844年,J.リウビルは, は超越数であることを示し,超越数が無限にあることを初めて証明した。その後,G.カントルは集合論を建設し,濃度の概念を用いて超越数は代数的数よりはるかに多いことを77年に示してセンセーションを巻き起こした。…
は超越数であることを示し,超越数が無限にあることを初めて証明した。その後,G.カントルは集合論を建設し,濃度の概念を用いて超越数は代数的数よりはるかに多いことを77年に示してセンセーションを巻き起こした。…
※「リウビル」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
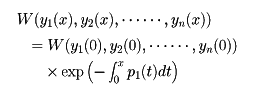


 は超越数であることを示し,超越数が無限にあることを初めて証明した。その後,G.カントルは集合論を建設し,濃度の概念を用いて超越数は代数的数よりはるかに多いことを77年に示してセンセーションを巻き起こした。…
は超越数であることを示し,超越数が無限にあることを初めて証明した。その後,G.カントルは集合論を建設し,濃度の概念を用いて超越数は代数的数よりはるかに多いことを77年に示してセンセーションを巻き起こした。…