解析関数（読み）かいせきかんすう

日本大百科全書(ニッポニカ)

解析関数
かいせきかんすう

複素平面の領域D上の複素関数f(z)が、D内の点cの近くの各点で微分可能なとき、関数はcにおいて正則であるという。このとき、cの近くでテーラー展開ができて、
　　f(z)＝c₀＋c₁(z－c)＋c₂(z－c)²
　　　　 ＋……＋c_n(z－c)ⁿ＋……
の形で表せる。逆に、関数がこの形の整級数で表せるとき、関数は点cで解析的であるといい、領域D内の各点で解析的な関数をDでの解析関数という。さて、右辺の整級数が収束するようなzでは、級数の表す関数は何回でも微分可能となる。したがって、点cの近くでは正則性と解析性は同値である。

［洲之内治男］

解析接続

領域D₁上で正則な関数f₁(z)と、D₂上で正則な関数f₂(z)が与えられ、D₁∩D₂（D₁とD₂の共通部分）に含まれるある領域D₀上でf₁(z)＝f₂(z)となるとき、D₁∪D₂（D₁、D₂の和集合）上に一つの正則関数

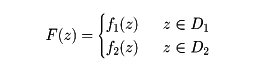
が決まることは正則関数の一致の定理よりわかる。このとき、F(z)はf₁(z)（またはf₂(z)）の解析接続であるという。いま、領域D上の正則関数f(z)から始めて、解析接続を次々に繰り返して、最終的に得られる関数を解析関数という。このとき、解析関数の境界を越えて解析接続はできない。実変数の実関数がテーラー展開できるとき、その関数は実解析的という。実解析的な関数は複素変数の解析関数に拡張できる。したがって実解析的な関数論は関数論のなかで統一的に取り扱うことができる。

［洲之内治男］

[参照項目] | 関数論 | テーラー展開

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

解析関数 (かいせきかんすう)
analytic function

二通りの意味がある。一つは（1価な）正則関数の別称である。もう一つは，以下に説明するように，多価な正則関数を表すための関数要素の集合に対する名称である。

　複素平面の点aを含むある領域で定義された正則関数を，aにおける関数要素と名付ける。aにおける二つの関数要素がaのある近傍で一致するとき，これらは同値であると呼び，同値類をaにおける正則関数芽germ of holomorphic functionという。次に0≦t≦1である各tに，点a（t）における正則関数芽を対応させ，t→a（t）は曲線Cとなり，またtごとに，a（t）における芽に属する関数要素をとり出してきたとき，要素全体が曲線Cに沿っての解析接続となっている場合，これを正則関数芽の曲線という。

　正則関数芽の集合で，（1）任意の二つの元は必ず曲線で結べる，（2）この性質をもつ極大集合である，という2条件を満たすものを，（ワイヤーシュトラスの意味の）解析関数という。一つの解析関数において，aを中心とした正則関数芽に対し，そこの値を考えることによって，多価な，そして局所的には1価な関数が得られる。関数論における多価な正則関数というものは，このようなものとして系統的に扱うことができる。
執筆者：及川 廣太郎

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

解析関数
かいせきかんすう
analytic function

実変数 x の関数 f(x) あるいは複素変数 z の関数 f(z) が，それぞれの定義域内のすべての点で解析的である，すなわちそこでべき級数に展開できるとき，f(x) あるいは f(z) は，それらの定義域における解析関数という。

出典　ブリタニカ国際大百科事典 小項目事典