求積法（読み）キュウセキホウ（英語表記）quadrature

デジタル大辞泉

きゅうせき‐ほう〔キウセキハフ〕【求積法】

不定積分を有限回行うことによって微分方程式の解を求める方法。

出典　小学館

精選版 日本国語大辞典

きゅうせき‐ほうキウセキハフ【求積法】

1. 〘 名詞 〙 不定積分を有限回行なうことによって、微分方程式の解を求める方法。求積。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

求積法 (きゅうせきほう)
quadrature

古くは，図形の面積や体積を求めることをいい，アルキメデスの研究などがある。17世紀になって微積分学ができてから以後は，微分方程式の解を，代数的演算，変数変換，積分を有限回用いることによって求める方法を求積法というようになった。一般の微分方程式は求積法で解を求めることができない。求積法で解ける微分方程式はむしろ例外といってよい。以下，常微分方程式を使って求積法で解ける形をいくつかあげておこう。

（1）変数分離形dy/dx＝p（x）q（y）　これは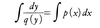，の形に解くことができる。

（2）同次形dy/dx＝f（y/x）　これはy＝xuとおいて変数をyからuに変換することにより，変数分離形du/dx＝（f（u）－u）/xに帰着できる。

（3）線形dy/dx＝p（x）y＋q（x）　これの一般解は，次式によって与えられる。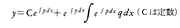（4）ベルヌーイの方程式dy/dx＝p（x）y＋q（x）yⁿ　n＝0，1のときは線形である。n≠1のときは，y¹⁻ⁿ＝uとおくとuに関する線形方程式に帰着される。

（5）完全微分形　微分方程式をf（x，y）dx＋g（x，y）dy＝0の形に書いたとき，条件f_y（x，y）＝g_x（x，y）が成り立つものをいう。このときは関数F（x，y）でF_x＝f，F_y＝gとなるものが存在し，解はF（x，y）＝C（Cは定数）の形で与えられる。

　高階の常微分方程式を使って求積法で解けるものはほとんどないが，定数係数の線形方程式，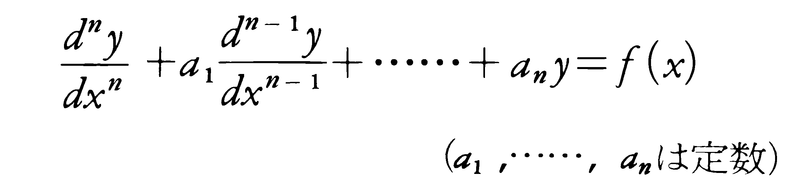

は求積法で解くことができる。n＝2，すなわち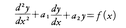，の場合には次のようになる。

　二次方程式λ²＋a₁λ＋a₂＝0の根をλ₁，λ₂とすると，λ₁≠λ₂のときは，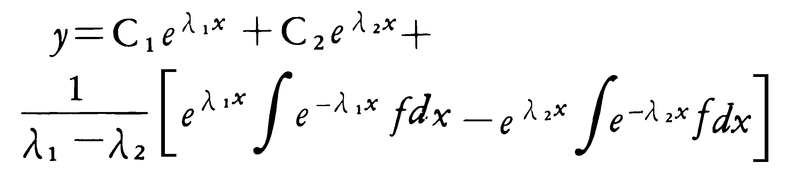

λ₁＝λ₂のときはλ₁＝λ₂＝λとおくと，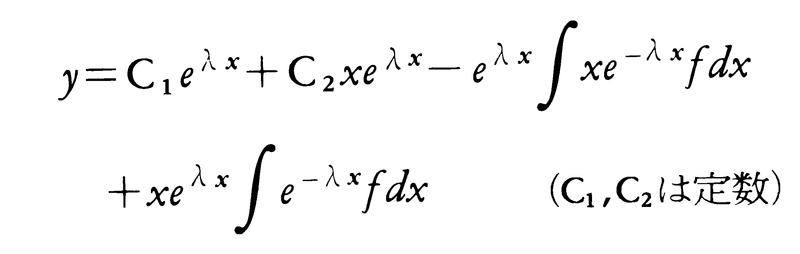


執筆者：斎藤 利弥

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

求積法【きゅうせきほう】

元来は線の長さ，図形の面積・体積を求める計算法。現在ではおもに，微分方程式を不定積分によって解くことをいう。→積分

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

求積法
きゅうせきほう
mensuration; quadrature

2つの異なった意味で用いられる。1つは，図形の長さ，面積および体積を，近似値を求める場合も含めて，計算する方法 mensurationをいい，他の1つは，特殊な形の微分方程式を解く場合に，不定積分を有限回行うことによって，その解を求める方法 quadratureをいう。

出典　ブリタニカ国際大百科事典 小項目事典