無限小（読み）ムゲンショウ（英語表記）infinitesimal

デジタル大辞泉

むげん‐しょう〔‐セウ〕【無限小】

１ 限りなく小さいこと。
２ 数学で、変数が限りなく零に近づくこと。また、その変数。⇔無限大。

出典　小学館

精選版 日本国語大辞典

むげん‐しょう‥セウ【無限小】

1. 〘 名詞 〙
2. ① ( 形動 ) 限りなく小さいこと。小ささが限りないこと。また、そのさま。
   1. [初出の実例]「その針の先端のような一点で、無限小の微粒子に化すと同時に」(出典：死霊‐二章（1946‐48）〈埴谷雄高〉)
3. ② 数学で、変数ｘの絶対値がどんなに小さな正数よりもなお小さくなる場合の、その変数ｘの状態のこと。記号 x→0 を用いて表わす。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

無限小
むげんしょう
infinitesimal

関数f(x)について、x→a（またはx→a+0,x→a-0,x→∞など）のときf(x)→0となるならば、x→aのときf(x)は無限小であるという。

　二つの無限小f(x),g(x)に対して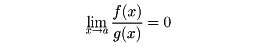

ならばf(x)はg(x)より高位の無限小であるといい、これをf(x)=o(g(x))と書き表す。また、x=aの近傍でf(x)/g(x)が有界のとき、これをf(x)=O(g(x))と書き表す。記号o、Oはランダウの記号とよばれている。また、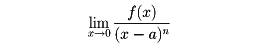

が存在して0でないとき、f(x)の無限小の位数はnであるという。

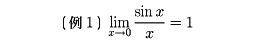
であるから、x→0のとき、sin xは1位の無限小である。1-cos xは2位の無限小、log(1+x)は1位の無限小である。

　f(x)がx=aの近傍で定義され、そこでn回微分可能ならば、f(x)のテーラー展開は、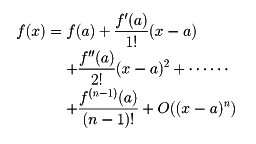

と書くことができる。そして、f(a)=0ならば、x→aのときf(x)は無限小であるが、このとき、f(a),f′(a),f″(a),……のうち、初めて0でないものf^(k)(a)について、f(x)はk位の無限小となる。

〔例2〕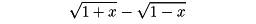

はx→0のとき無限小であるが、二項定理により、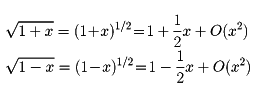

であるから、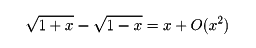

となり、これは1位の無限小であることがわかる。

　f(x),g(x)がともに無限小のとき、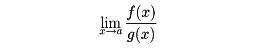

を不定形の極限値という。このときf(x),g(x)にテーラーの定理を適用して、極限値を求めることができる。また、ロピタルの定理というのが著名である。

〔例3〕x→0のとき、cosx＝1－1/2x²+O(x⁴)であるから、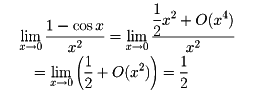

［竹之内脩］

[参照項目] | テーラー展開 | ロピタルの定理

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

無限小【むげんしょう】

複素値関数fが（式１）となるとき，fをaにおける無限小という。２つの無限小f，gに対して，f/gが無限小であるとき，fはgより高位の無限小（gはfより低位の無限小）という。また，f/g(n/)が０でない有限値をとるとき，fはgに関してn位の無限小という。
→関連項目ウォリス

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

無限小
むげんしょう
infinitesimal

数学において，ある変数が0に収束するとき，その変数は無限小になるといい，無限小になる変数を，単に無限小という。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の無限小の言及

【無限大･無限小】より

…＋∞を単に∞と書き，無限大と呼ぶこともある。実数列｛x_n｝があって，n→∞のとき，x_n→∞となるならばx_nは(正の)無限大になるといい，x_n→－∞となるならばx_nは負の無限大になるといい，またx_n→0となるならばx_nは無限小になるという。x_nが正または負の無限大になるならば1/x_nは無限小となる。…

※「無限小」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」