素数定理（読み）ソスウテイリ（英語表記）prime number theorem

デジタル大辞泉

そすう‐ていり【素数定理】

整数論における素数についての定理の一。π（x）をxより大きくない素数の個数とすると、x→∞に対し、π（x）はx/log xと近似できる。logは底eの自然対数。ドイツの数学者ガウスが、となり合う素数同士の平均間隔は、およそその桁数に比例することを示した。

出典　小学館

改訂新版　世界大百科事典

素数定理 (そすうていり)
prime number theorem

実数xに対してπ（x）でp≦xとなる素数pの個数を表すことにする。例えば，π（10）＝4，π（100）＝25，……，π（100000000）＝5761455である。xが増大するとともにπ（x）は増大していくのだが，その増大の程度がx/log xであるということ，正確にいうと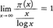，であるというのが素数定理である。素数の現れ方がきわめて不規則であることを思えば，注目すべき事実といわなければならない。これは，C.F.ガウスによって予想されたが，約100年後の1896年にJ.アダマールとド・ラ・バレ・プーサンC.de la Vallée Poussinによりほぼ同時に証明された。π（x）がG.F.リーマンのゼータ関数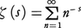，と密接に関係しているというリーマンの深い着想と，一変数解析関数論の発展とによって証明されたものである。1949年にはセルバーグA.Selbergによって一変数解析関数の理論を用いない初等的な証明が与えられた。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

素数定理
そすうていり
prime number theorem

自然数 x をこえない素数の個数を π(x) で表わすと，π(x) は x が大きければ x/ log x によって与えられ，求められる近似値は x が大きくなるほどより真の値に近づく，言い換えれば，π(x) は x→∞ のとき，x/ log x との比が1に近づく。これを素数定理という。これは，C.F.ガウスが少年の頃に予測してから，19世紀を通じて大きな課題になっていた。これについては，1850年代に P.チェビシェフが初めて両者の比が上下に有界なことを示したが，最終的な証明は，J.アダマールとベルギーの数学者 C.ド・ラ・バレ＝プーサンによって，ほとんど同時に (1896) ，ほとんど同じ方法でなされた。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

素数定理【prime number theorem】

π（x） を x よりも大きくない素数の個数としたとき，[π（x）]（lnx）/x は x が無限大の極限において1となる，という定理．

出典　朝倉書店