累乗根（読み）ルイジョウコン

デジタル大辞泉

るいじょう‐こん【累乗根】

累乗してaとなる数をaの累乗根という。すなわち、nを2以上の自然数としたとき、xⁿ＝aとなる数xを、aのn乗根とよぶ。とくに二乗根、三乗根はそれぞれ平方根、立方根ともいう。乗根。羃根べきこん。冪乗根べきじょうこん。

出典　小学館

精選版 日本国語大辞典

るいじょう‐こん【累乗根】

1. 〘 名詞 〙 その累乗がａになる数のａに対する称。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

累乗根
るいじょうこん

nを2以上の整数とするとき、n乗してaになる数、つまり、xⁿ=aとなる数xを、aのn乗根といい、二乗根、三乗根、……を総称して、aの累乗根という（べき根ともいい、羃根(べきこん)、巾根(べきこん)とも書く）。aの二乗根（平方根）、三乗根（立方根）は累乗根の一つといえる。

　実数の範囲で考えるとき、次のことがいえる。nが奇数のとき、実数aに対して、aのn乗根はただ一つある。これを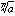と表す。nが偶数のとき、正の数aに対して、aのn乗根は正・負一つずつある。その正のほうを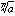と表す。負のほうは-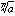となる。とくにnが2の場合は、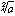と書かずに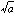と書く。また、nが偶数のとき、負の数aのn乗根は存在しない。

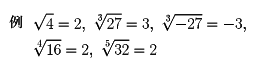
　正の数a、bの累乗根については、次の法則が成り立つ。

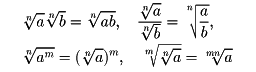
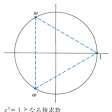
　以上は実数の範囲での累乗根である。いま複素数の範囲で考えると、0と異なる数に対して、そのn乗根は、ちょうどn個存在する。とくに、1のn乗根を考えると、n個あり、それらは複素平面上で表すと、原点を中心とする半径1の円周上にあって、1を一つの頂点とする正n角形の頂点となる。

［三輪辰郎］

[参照項目] | 累乗

複素数の範囲での累乗根

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

累乗根
るいじょうこん
root

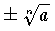方程式 xⁿ＝a（a は実数）を満足する x の値を，a の（正の）n 乗根といい，これを a^1/n と表す。a の n 乗根の個数は，範囲を複素数にまで広げて考えれば一般に n 個ある。a の n 乗根のうち実数値をとるものは，(1) a が正，n が偶数のとき ，(2) a が正，n が奇数のとき 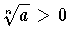，(3) a が負，n が偶数のとき，存在しない，(4) a が負，n が奇数のとき 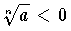，の四つの場合にかぎられる。一方 a が 0でない複素数のとき，方程式 xⁿ＝α（α≠0）を満足する複素数 x は，α＝a＋ib を表す点（a，b）の極表示に関する動径を r，偏角をθとするとき，絶対値が r の n 乗根，偏角がθ/n およびそれに 2π/n の整数倍を加えた合計 n 個の極座標で表される値である。（→累乗）

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

累乗根 (るいじょうこん)

→冪（べき）根

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の累乗根の言及

【べき根(冪根)】より

…とくにn＝2,3のとき，それぞれ平方根，立方根とも呼ぶ。aの2乗根，3乗根，……，n乗根をaのべき根または累乗根という。aが正の数のとき，aはただ一つ正のn乗根をもつ。…

※「累乗根」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」