精選版 日本国語大辞典 「立方根」の意味・読み・例文・類語
りっぽう‐こんリッパウ‥【立方根】
- 〘 名詞 〙 ある数aを立方するとbになるときのaのbに対する称。bの立方根を記号で3√bと書く。たとえば、2は8の立方根である。三乗根。〔改正増補和英語林集成(1886)〕
改訂新版 世界大百科事典 「立方根」の意味・わかりやすい解説
立方根 (りっぽうこん)
cubic root
3乗してaとなる数を,aの立方根,または3乗根という。とくに,aが実数のとき,x3=aを満たす実根xは,つねにただ一つあり,3\(\sqrt{a}\)で表す。例えば, 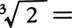
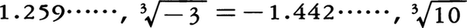
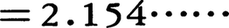 などである。しかし,平方根の場合とは異なり,与えられた実数aの3乗根を,定規とコンパスを用い作図により求めることは,一般には必ずしも可能ではないことが証明されている。とくに,3\(\sqrt{2}\)(つまり,体積2の立方体の1辺の長さ)を,作図により求める問題は,古代から〈立方倍積問題〉,あるいは〈デロスの問題〉と呼ばれ,三大作図不能問題の一つとして有名である。
などである。しかし,平方根の場合とは異なり,与えられた実数aの3乗根を,定規とコンパスを用い作図により求めることは,一般には必ずしも可能ではないことが証明されている。とくに,3\(\sqrt{2}\)(つまり,体積2の立方体の1辺の長さ)を,作図により求める問題は,古代から〈立方倍積問題〉,あるいは〈デロスの問題〉と呼ばれ,三大作図不能問題の一つとして有名である。
一般の0でない複素数αについて,αの立方根はすべて複素数で3個ある。1の立方根は,
x3-1=(x-1)(x2+x+1)=0
により,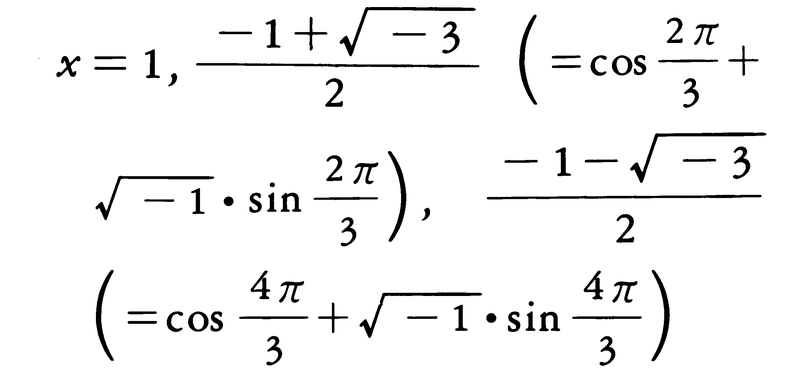
を得る。後の二つを1の虚立方根といい,そのいずれか一つをωで表すと,他はω2となり,1+ω+ω2=0を満たしている。さらに,0でない複素数αの立方根の一つをβとすると,αの立方根はβ,βω,βω2の3個である。
開立
実数aの,実数の範囲での立方根を求めることを,aを立方に開く,またはaを開立するといい,その計算の方法を開立法という。開立法は,立方の公式,
(x+y)3=x3+3x2y+3xy2+y3
を利用する。すなわち,aを正の数とするとき,
(1)3乗すればaより小で,aに近い正の数b1をとる。
(2)3\(\sqrt{a}\)-b1=c>0とすれば,
a=b13+3b12c+3b1c2+c3
である。ここで,cはb1に比べて小さいから,3b1c2+c3を無視することにより,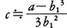 となる。
となる。
(3)そこで,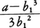 に近く,これより小さい正の数c1をとる。b2=b1+c1とすれば,b2はb1より,さらに3\(\sqrt{a}\)に近づく。
に近く,これより小さい正の数c1をとる。b2=b1+c1とすれば,b2はb1より,さらに3\(\sqrt{a}\)に近づく。
(4)次に,b1の代りにb2を用い,(2)(3)の操作を行い,b3を求める。
(5)以下,(2)(3)(4)を繰り返し,b4,b5,……を求めていけば,n回目にbn=3\(\sqrt{a}\)となるか,nが大きくなるにつれ,bnは限りなく3\(\sqrt{a}\)に近づく。
例えば,a=12977.875のとき,まず小数点を基準にして,3桁ずつにくぎる。
12・977・875・
(1)これから,aの立方根の整数部分が,2桁であることを知り,b1=20としてよいことがわかる。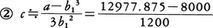 から,c1=3。
から,c1=3。
(3)b2=b1+c1=20+3=23。
(4)以下,計算を続ける……。
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「立方根」の意味・わかりやすい解説
立方根
りっぽうこん
cubic root
1,
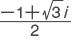 ,
,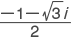
である。ここで,
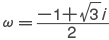 とおくと,
とおくと,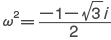 となる。ωとω2はともに 3乗してはじめて 1になる複素数であり,1の原始三乗根と呼ばれる。複素数 1,ω,ω2はガウス平面(複素数平面)において,正三角形の三つの頂点となる。一般に実数 a に対して,z3=a を満たす複素数は
となる。ωとω2はともに 3乗してはじめて 1になる複素数であり,1の原始三乗根と呼ばれる。複素数 1,ω,ω2はガウス平面(複素数平面)において,正三角形の三つの頂点となる。一般に実数 a に対して,z3=a を満たす複素数は  ,
,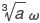 ,
,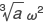 である。古代ギリシアの三大作図問題(→作図)の一つに「与えられた立方体の体積の 2倍の体積をもつ立方体をつくること」があるが,これは定規とコンパスによって立方根を作図できるかという問題になる。定規とコンパスで作図できる数は,有理数から出発して,その平方根をとる操作および加減乗除(→四則)の操作を繰り返して得られる数であることが示されるので,一般には立方根は作図できないことがわかる。
である。古代ギリシアの三大作図問題(→作図)の一つに「与えられた立方体の体積の 2倍の体積をもつ立方体をつくること」があるが,これは定規とコンパスによって立方根を作図できるかという問題になる。定規とコンパスで作図できる数は,有理数から出発して,その平方根をとる操作および加減乗除(→四則)の操作を繰り返して得られる数であることが示されるので,一般には立方根は作図できないことがわかる。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「立方根」の意味・わかりやすい解説
立方根【りっぽうこん】
出典 株式会社平凡社百科事典マイペディアについて 情報
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

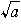 と表す。例えば、
と表す。例えば、