日本大百科全書(ニッポニカ) 「結び糸」の意味・わかりやすい解説
結び糸
むすびいと
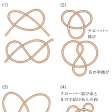
空間の中で1本の紐(ひも)を自由自在にぐるぐると自分自身に巻き付け、結び付けて、その両端を縛ってできる図形が結び糸(結び目)である。たとえばの(1)は紐で物を縛るときによくつくる結び目の図形であるが、これらの両端をあわせたの(2)のクローバー結びや、8の字結びのような空間図形が結び糸である。こうした結び糸K1は、自分自身を切ったりくっつけたりしないで、空間の中で自然に伸ばしたり縮めたりなどの変形をして結び糸K2になるとき、K1とK2は同じ結び糸であるという。
これは正確には、空間R3を自分の上へ写すh(K1)=K2となるような(向きを保つ)同相写像hが存在することであると述べられる。たとえばの(2)で、クローバー結びの糸のどこか1か所で上下の交差を逆にした結び糸は、の(3)のように(平面に描かれた)円周が示す結んでいない(平凡な)結び糸と同じである。しかし、元のの(2)のクローバー結び糸や8の字結び糸は、どのようにくふうしても、解けてしまって平凡な結び糸になることはないし、またクローバーが8の字になることもない、互いに異なる結び糸である。
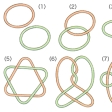
二つの結び糸は、の(4)のように加えて、それらより複雑な和の結び糸をつくることもできるし、同じ結び方を無限に繰り返して(しだいに結び目は小さくなり、ついに1点に収束する)非常に複雑な結び糸を考えることもできる。
そこで結び糸理論では、二つの結び糸の和とはならず、また無限には結び方を繰り返さない互いに異なる結び糸はどのくらいあるのか、それらを区別するのにはどんな概念を考えればよいかという点について研究が行われている。
たとえば、結び糸Kに対してその補空間の基本群π1(R3-K)が整数の群Zと同型であることが、Kが平凡な結び糸となる必要十分条件であることが知られているし、または、それぞれ他の和とはならない結び糸を、その上下交差点の個数の少ない順に示したものである。現在でも、結び糸の問題は完全には解かれていない難問である。
[野口 廣]
絡み糸(組み糸)
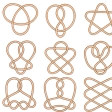
空間の中で自分自身結んでいる結び糸を数個互いに絡ませてできる図形が絡み糸である。は2個の結び糸を絡ませた絡み糸である。結び糸と同様に切ったり、はり合わせたりしないで自然に他へ変形できるとき同じ絡み糸と定めるが、(2)より(7)まではすべて異なる絡み糸である。
[野口 廣]