非線形方程式（読み）ヒセンケイホウテイシキ（その他表記）nonlinear equation

デジタル大辞泉

ひせんけい‐ほうていしき〔‐ハウテイシキ〕【非線形方程式】

2次以上の項を含む方程式、および未知関数についての関数方程式・微分方程式・積分方程式。通常、厳密解を得ることが困難な場合が多い。一部、適切な変数変換や変数分離を行うことによって線形方程式に移行し、解を求めることができる。

出典　小学館

改訂新版　世界大百科事典

非線形方程式 (ひせんけいほうていしき)
nonlinear equation

線形でない方程式を総称して非線形方程式という。微分方程式の場合，それが線形であるとは，方程式が未知関数およびそれの導関数について一次式であることだから，例えば常微分方程式，

　dx_j/dt＝f_j（t，x₁，……，x_n）

　　　　　　　　　　　（j＝1，……，n）

においてf_jがx₁，……，x_nの一次式であるとき以外は方程式はつねに非線形である。非線形方程式は線形方程式に比べて解の性質が複雑で，したがってその理論も線形の場合に比べて不完全である。

　線形方程式の場合には，すべての解が共通の定義域をもち，それは微分方程式の右辺が連続であるようなtの範囲と一致する。これに対して非線形方程式にあっては，解の定義域が解ごとに異なるのがふつうであり，またtが有限の範囲で解が有界でなくなってしまう，いわゆる爆発現象を起こすことが多い。非線形方程式の解の大域的研究においては，このことが最大の難点となる。

　非線形性は線形性の否定概念であるから，非線形方程式に対して特別に有効な一般理論というものは存在しない。いろいろな特殊な場合についてそれぞれの理論が開発されている。例えば非線形振動論，複素領域における非線形微分方程式の特異点の理論などがそれで，多くは非線形方程式を線形方程式で近似する，線形近似の理論である。
執筆者：斎藤 利弥

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の非線形方程式の言及

【微分方程式】より

…また境界値問題についても多くのことが知られている。　非線形方程式の研究は線形の場合に比べて多くの困難を伴う。正規形の非線形方程式(1)の解が一つ求められたとし，それをx_j＝φ_j(t)(j＝1，……，n)とするとき，この解の近傍にある他の解を調べるには，ふつう変数変換x_j＝φ_j(t)＋y_jを行って(1)を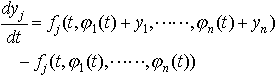，と変形する。…

※「非線形方程式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」