日本大百科全書(ニッポニカ) の解説
ナビエ‐ストークス方程式
なびえすとーくすほうていしき
Navier-Stokes equations
流体力学において、粘性による効果も取り入れた流体の運動を表す方程式。フランスのナビエにより導かれたもので、のちにイギリスのストークスによって正しい形に整えられた。ある時刻(t)でのある場所(x、y、z)の流体の速度をv(vx、vy、vz)、流体の密度をρ、流体の圧力をp、単位質量当りの外力をf(fx、fy、fz)、粘性率をμ(一定)、圧縮率をΘとすると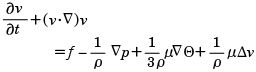
と表される。縮まない流体(非圧縮性流体)(Θ=0)の場合、この方程式は
と簡略になる。また、粘性率μ=0である場合、完全流体の運動方程式であるオイラー方程式になる。ナビエ‐ストークス方程式は非線形であるため、いくつかの特殊例を除いて厳密解がなく、線形近似により解くくふうがなされている。また、この方程式と流体の状態方程式p=f(ρ)と連続の方程式∂ρ/∂t+∇・(ρv)=0を組合せ、適切な境界条件と初期条件により流体の運動を数値的に計算する試みが続いている。
[山本将史 2022年4月19日]


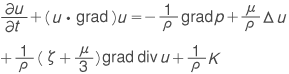 ただし,Δ≡div grad は
ただし,Δ≡div grad は