オイラー（読み）おいらー（英語表記）Leonhard Euler

デジタル大辞泉

オイラー（Ulf Svante von Euler）

［1905～1983］スウェーデンの生理学者。オイラー＝ケルピンの子。ノルアドレナリンを発見し、神経伝達物質であることを確認した。B＝カッツ、J＝アクセルロッドとともに1970年にノーベル生理学医学賞を受賞。

オイラー（Leonhard Euler）

［1707～1783］スイスの数学者。解析学など数学の諸分野での膨大な研究のほか、医学・化学・天文学などでも功績がある。著「無限小解析入門」「力学」など。

出典　小学館

精選版 日本国語大辞典

オイラー

1. ( Leonhard Euler レオンハルト━ ) スイスの数学者。微積分学を発展させ、変分学を創始。天文学、力学などの分野でも活躍した。（一七〇七‐八三）

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

オイラー（Leonhard Euler）
おいらー
Leonhard Euler
（1707―1783）

18世紀最大の数学者。スイスのバーゼルに生まれる。ヨハン・ベルヌーイに数学を学び、1727年、当時ペテルブルグにいたヨハンの息子のニコラスNicholas（1695―1726）とダニエルに招かれ、1741年まで同地で研究を続けた。同年ベルリン科学アカデミーに移ったが、1766年エカチェリーナ2世（在位1762～1796）に招かれてペテルブルグに行き、終生その地で研究を続けた。1738年ごろ右眼の視力を失い、晩年には両眼とも失明したが、非凡な記憶力と助手の協力で超人的な研究活動を続けた。論文は死後発表されたものまで含めて850編に達し、全87巻の予定の全集は、2007年までに70巻以上が刊行されたが、なお完結していない。

　業績は多方面にわたり、帆船のマストの配置や、耳の生理学の研究もあるが、そのすべては広義の数学に関連し、半分近くは解析学およびその応用としての力学、天体力学、数理物理学関係のものである。主著『力学』、『無限小解析入門』（2巻）において、今日の微分積分学の教科書にある多くの計算法を総合し、複素数を形式的に使って、オイラーの公式e^iv＝cosv＋isinvをはじめ、多くの公式を巧妙に求め、またオイラーの角を定義し、二次曲面の標準形の分類を行った。三角法や年金の問題など、オイラーがまとめて以後、本質的な発展のみられない分野もある。

　数学の他の分野でも、整数論においてオイラーの関数（mより小さい数でmと互いに素な正整数の個数）、法mに関する原始根(こん)などの重要な研究がある。またケーニヒスベルクの橋渡りの問題からトポロジーを創始し、多面体のオイラーの公式を示した。そのほか、オイラーの定数、Γ(ガンマ)関数とΒ(ベータ)関数、変分法など彼の名を冠する有名な成果が多い。応用面では、太陰運動論に初めて計算可能な解を発案し、月の運動表計算に対する方法発明賞をイギリス海軍から授けられたりもした。

　オイラーの業績に関して、たとえば級数の収束などについて、19世紀以降反省されるようになった「厳密性への関心」が少ないといわれるが、それはかならずしも当を得た批判とはいいがたい。不合理であるものを正当化するために、ときとして不自然な「説明」を探し求めたことがあり、また組合せ論に関する予想など近年否定的に解決されたものもあるが、むしろ彼の業績全般にわたって、巧妙な解析学の技術にその特徴があるといえそうである。

［一松　信］

[参照項目] | オイラーの定数 | 解析学 | トポロジー | ベルヌーイ | ベルヌーイ

オイラー（Ulf Savante von Euler）
おいらー
Ulf Svante von Euler
（1905―1983）

スウェーデンの生理学者。ストックホルム大学カロリンスカヤ研究所医学部を1930年に卒業、母校で研究を続け、1939年に生理学教授。スウェーデン王立学士院会員。1966年からノーベル財団総裁。1946年に副腎(ふくじん)から分泌されるノルアドレナリンを発見、その生理作用の研究から、この物質が交感神経の伝達物質であることを確認した。この研究によってアクセルロッド、カッツとともに1970年にノーベル医学生理学賞を受賞した。1929年にノーベル化学賞を受賞したオイラー・ケルピンは彼の父である。

［宇佐美正一郎］

[参照項目] | アクセルロッド | アドレナリン | オイラー・ケルピン | 化学伝達物質 | カッツ

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

オイラー
Leonhard Euler
生没年：1707-83

スイスのバーゼルに生まれ，その地の大学のヨハン・ベルヌーイに数学の能力を認められた。18世紀においては，第一線の科学者は絶対主義王権のもとで科学アカデミーに所属して研究活動に専念するのがつねであり，オイラーもペテルブルグ，ベルリンの科学アカデミーで活躍した。1735年に1眼の明を失い，さらに66年には全盲になったが，多産な計算をし続け，その著作，論文，遺稿は1911年以降《全集》としていまだに刊行中である。1748年の名教科書《無限解析序論》は，簡明な記号を用いて代数学，微分積分学，三角法を記述し，ラグランジュ，ラプラス，ガウスらの従うところとなった。《微分計算教程》（1755），《積分計算教程》（1768-74）も大きな影響力をもった。1744年刊の《与えられた性質を有する極大・極小曲線を見いだす方法》は，独創的な変分法の書であり，いわゆるオイラーの方程式が導きだされている。応用数学の諸分野でも多産で，《力学》（1736）はニュートン力学をライプニッツ的微分積分学で書き換える試みであり，ほかにも剛体力学，天体力学，水力学に関して解析学的計算を展開した。オイラーはまた，ケーニヒスベルクの七つの橋の問題（一筆書き），多面体論などで重要な貢献を行った。しかし，〈無限〉の数学的扱いにおいてはしばしば不注意な計算に走り，19世紀の数学者（とくに，コーシーら）の厳密な再定式化の試みによって吟味されなければならなかった。無明のオイラーは，光の世紀，啓蒙の時代の最大の数学者であった。
執筆者：佐々木 力

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

オイラー

スイス生れの数学者。バーゼル大学でジャン・ベルヌーイに学び，1730年ペテルブルグ・アカデミー教授，1741年フリードリヒ２世に招かれベルリン・アカデミー数学部長となる。1766年ペテルブルグに帰り，失明にも屈せず研究を続け同地で死去。微積分学を発展させ，変分学を創始，代数，整数論，幾何学にも大きな業績を残した。また水力学，剛体力学，三体問題，潮汐(ちょうせき)，振動，音響，色消しレンズなど多方面の研究がある。→オイラーの定理
→関連項目ケーニヒスベルクの橋の問題｜整数論｜フルネーロン｜流体力学

オイラー

スウェーデンの生理学者。父はオイラー・ケルピン。ストックホルム医科大学卒。1939年以降国立カロリンスカ研究所教授。交感神経の興奮によって神経末端から遊離されるのがアドレナリンからメチル基をとったノルアドレナリンであることを解明。1953年―1965年ノーベル生理医学賞選考委員，1966年からノーベル財団理事長。1970年B.カッツ，J.アクセルロッドとともにノーベル生理医学賞。

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

オイラー
Euler， Leonhard

[生]1707.4.15. バーゼル
[没]1783.9.18. ペテルブルグ
スイスの数学者。 18世紀を通じ最も多才な数学者で，近代解析学の創始者の一人。 J.ベルヌーイのもとで学び，1730年にペテルブルグ科学アカデミーの物理学教授，33年に数学教授となる。 41年ベルリン科学アカデミー会員。過度の仕事によりまもなく片方の目の視力を失い，晩年には残りの一方も失明したが，学問に対する熱意は少しも衰えなかった。 66年再びペテルブルグに戻り，その地で没した。彼の業績は，純粋数学の分野に顕著であるが，物理学，天文学にも功績を残している。オイラーの名のつく慣用の記号や定理が，初等幾何学から高等解析学の分野にいたるまで多数存在する。三角関数の解析的取扱い，対数の算法的取扱い，楕円積分の加法定理の証明，整数論における平方剰余の相互法則その他の発見，微分幾何学，変分法，微分方程式への先駆的研究など多大の成果を残した。主著『無限小解析緒論』 (2巻，1748) ，『微分学原理』 (55) ，『積分学原理』 (3巻，68～70) 。

オイラー
Euler， Ulf Svante von

[生]1905.2.7. ストックホルム
[没]1983.3.10. ストックホルム
スウェーデンの生理学者。ノーベル化学賞を受けた H.オイラー＝ケルピンの子。カロリンスカ研究所の医学校卒業，1930年学位取得。カロリンスカ研究所生理学教授 (1939～71) ，スウェーデン王立アカデミー会員，ノーベル生理学・医学賞選考委員 (53～65) ，ノーベル財団理事長 (66) 。 48年にノルアドレナリンを発見するなど，40年代に，神経末梢部の伝達物質の発見とその貯蔵・解離・不活化の機構の解明など多くの研究成果を上げた。これらの業績に対して，70年に，J.アクセルロッド，B.カッツとともにノーベル生理学・医学賞が授与された。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内のオイラーの言及

【位相幾何学】より

…analysis situsという言葉は，20世紀初期まで長く通用していたが，今日この言葉は用いられない。
［位相不変量――オイラー標数］
　正多面体は5種類あり，すべて互いに同相である。どの正多面体についても，その頂点の数をa，辺の数をb，面の数をcとすると，a－b＋c＝2が成り立つ。…

【Γ関数】より

…解析学で重要な特殊関数。1929年，L.オイラーは定積分に関連して，次の無限乗積を複素数zに対し導入した。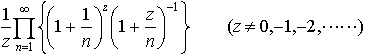これをA.M.ルジャンドルが，ガンマ関数と命名し，記号Γ(z)を用いた。…

【幾何学】より

…とくにデカルトはこの考えを彼の有名な著書《方法叙説》(1637)の付録の一つである《幾何学》において述べ，この方法は幾何学に発見性と統一性を与えることを強調した。解析幾何学は微積分学の発展に有力な基盤を与え，18世紀にはL.オイラーらによって著しく進展し，アポロニオスの円錐曲線論も二次曲線論として代数的に整理された。解析幾何学によって，数と図形とは本質的に別物ではなく，一方は他方の表現であるとの認識が得られた。…

【顕微鏡】より

…とくにレンズ系には収差の大きいものが用いられていたために有効な利用には限界があり，そのために，新発見の継続的な蓄積はなされず，17世紀から18世紀にかけて，顕微鏡観察での新しい発展は低迷していた。　しかし顕微鏡への期待は大きく，18世紀に入ってドイツのL.オイラー，イギリスのドロンドJ.Dollondらは，異種のガラスで作ったレンズを組み合わせることによって色収差を除く可能性があることを発見した。これは直ちに成果を生むことにはつながらなかったが，光学ガラスの研究と改良に見通しが与えられ，18世紀末(1791)に至ってオランダのビールドスナイダーF.Beeldsnijderによって色収差なしの複合レンズをもった高倍率の顕微鏡が初めて作られた。…

【ゴルドバッハ】より

…1726年ころの約2年間ロシア帝国学士院に地位を得，28年1月にモスクワへ移り，ピョートル2世およびアンナ王女の家庭教師となったが，32年にはロシア帝国学士院に戻った。また，この数年前からL.オイラーとの文通が始まり，それは63年まで続いた。1737年ころから政治家と接触することが多くなり，42年には外務省入りをして学士院との縁が切れたと同時に，数学から遠ざかった。…

【座屈】より

…座屈現象は，このような長柱だけでなく細長い断面のはりに曲げモーメントが働くときや薄い板の面内に圧縮力やせん断力が作用した場合にも生じ，建築，車両，船舶，航空機など長柱･薄板構造を使用する場合の座屈問題はとくに重要である。　なお，長柱の座屈に関してはL.オイラーの理論があり，断面の応力度が比例限度内にある場合の座屈荷重を与えるオイラーの長柱式が導かれている。【岩崎 正義】。…

【三体問題】より

…重心積分は3天体の重心が座標系に対して一様直線運動をすることを示し，角運動量積分は，3天体の座標原点に関する角運動量が一定に保たれること，そしてエネルギー積分は，3天体の全エネルギーが一定であることを示す。これら10個の積分は，すでにL.オイラーによって18世紀中ごろに発見されていて，オイラー積分，あるいは古典積分といわれるが，これらはn体問題でも成り立って三体問題に固有のものではない。　オイラー以後の三体問題の研究が新しい積分の発見に向けられたのは当然である。…

【数学】より

…　18世紀の初めには，ニュートンやライプニッツも活動していた。ライプニッツの便利な記号による微積分法は，ベルヌーイ兄弟らの協力によって幾何学，力学あるいは確率論の多くの問題に応用され，彼らに続くL.オイラーによりさらに発展させられた。オイラーは古今を通じもっとも多産な数学者の一人であり，代数計算にはことに巧みであった。…

【数学パズル】より

…この12種類を箱詰めにするとおもしろいパズルができ，図15‐cの6×10の長方形にペントオミノを入れると3776通りの入れ方がある。
［トポロジーパズル］
　点と線のつながり方を問題にするのがトポロジーパズルで，数学者のL.オイラーが1735年に提案した一筆書きの問題が最初である。ドイツのケーニヒスベルクは古い都で，18世紀の初めころは七つの橋が図16‐aのようにかかっていた。…

【整数論】より

…s(a)＞2a,s(a)＝2a,s(a)＜2aの三つの場合に従って，aは豊数(過剰数)，完全数，輸数(不足数)であるという。ユークリッドは，2^e－1が素数であれば2^e－1(2^e－1)は完全数であることを示したが，L.オイラーは偶数の完全数はこの形に限ることを示した。奇数の完全数は，いまのところ一つも知られていない。…

【超越数】より

…有理数係数のどんな代数方程式についてもその根にならない数，すなわち代数的数ではない数を超越数という。有理数から代数的操作で得ることができないという意味でL.オイラーが超越数と名付けた。彼は1748年ころ自然対数の底e，円周率πなどは超越数であろうと予想したが，eが無理数であることしか証明できなかった。…

【天体力学】より

…ただしニュートンは理論の展開をもっぱらユークリッド幾何学で行ったのでそこに適用の限界があった。　ニュートンの研究を受け継いで月の運動や三体問題などを解析的方法で論じたのはL.オイラーである。とくにケプラー要素の時間変化によって摂動を表す着想はオイラーに始まり(1753)，のちJ.L.ラグランジュが完成した(1782)。…

※「オイラー」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」