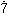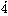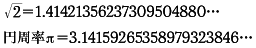精選版 日本国語大辞典 「無限小数」の意味・読み・例文・類語
むげん‐しょうすう‥セウスウ【無限小数】
- 〘 名詞 〙 小数点以下の桁数が限りなくつづく小数。循環小数と循環しない小数とに大別される。無窮小数。〔数学ニ用ヰル辞ノ英和対訳字書(1889)〕
日本大百科全書(ニッポニカ) 「無限小数」の意味・わかりやすい解説
改訂新版 世界大百科事典 「無限小数」の意味・わかりやすい解説
無限小数 (むげんしょうすう)
infinite decimal
2/3=0.666……のように無限に続く小数を無限小数といい,あるところで終わる小数を有限小数という。無限小数の中には,0.3121212……=0.312のようにあるところから先は同じ数字の配列が繰り返されるものがある。このような無限小数を循環小数という。循環小数は有理数を表すのだが,逆に有理数は有限小数か循環小数になる。したがって循環小数でない無限小数は有理数以外の数,つまり無理数である。例えば,\(\sqrt{2}\)や\(\sqrt{3}\)は有理数でないから,\(\sqrt{2}\)=1.41421356……や\(\sqrt{3}\)=3=1.7320508……は循環小数ではない。無限小数の中でも0.2999……のようにあるところから先は9が続くものは例外的であり,0.2999……は0.3と同じ実数を表し,有限小数と等しくなる。一方,有限小数は,0.12=0.11999……=0.119のように無限小数で表される。このように有限小数で表される数に限って二通りの小数による表示があり,他の数はただ一通りの小数による表示をもつ。したがって無限小数のみを考えることにすれば,実数と無限小数は1対1に対応する。
執筆者:斎藤 裕
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「無限小数」の意味・わかりやすい解説
無限小数
むげんしょうすう
「小数」のページをご覧ください。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の無限小数の言及
【小数】より
…1.75は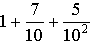 を表すが,このように有限で終わるものを有限小数という。1/7=0.142857142857……のように無限に続くものを無限小数という。無限小数のうち,上の例1/7の142857のように,あるところ以後は同じ数字の配列が繰り返されるものを循環小数という。…
を表すが,このように有限で終わるものを有限小数という。1/7=0.142857142857……のように無限に続くものを無限小数という。無限小数のうち,上の例1/7の142857のように,あるところ以後は同じ数字の配列が繰り返されるものを循環小数という。…
※「無限小数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


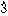
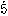 6
6