無理数（読み）ムリスウ（英語表記）irrational number

デジタル大辞泉

むり‐すう【無理数】

実数のうち、有理数でない数。二つの整数の比で表すことができない数。⇔有理数。

出典　小学館

精選版 日本国語大辞典

むり‐すう【無理数】

1. 〘 名詞 〙 実数のなかで分数の形で表わすことのできない数。⇔有理数。
   1. [初出の実例]「有理数を表さない無限小数の表すべき数を無理数といふ習慣になってゐる」(出典：零の発見（1939）〈吉田洋一〉二八)

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

無理数
むりすう
irrational number

有理数でない実数を無理数という。

　aが自然数で、a=b²（bは自然数）というようになっていなければ、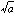は無理数である。このことを、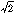の場合について検証する。

　いま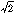が有理数q/pであるとする。ここに、p、qは互いに素（つまり、公約数がない）、としておく。

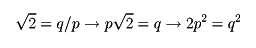
したがってqは偶数である。そこでq=2q′とすれば、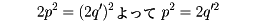

　これからpも偶数であることになるが、これはpとqが互いに素であるとした仮定に反する。ゆえに、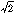は有理数ではない。つまり無理数である。

　次に、自然対数の底eが無理数であることを示そう。

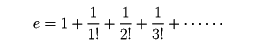
と表される。

　いま、eが有理数q/pであるとする。eは整数ではないから、p≧2である。そうすると、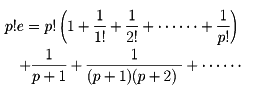

　左辺p!eおよび右辺の大括弧(かっこ)付きの項は整数である。そして、p+1＜p+2＜……だから、右辺の第2項以降の無限級数は、

より小さく、整数とはならないから、これは矛盾である。ゆえに、eは有理数ではない。つまり、無理数である。

　一般に、ある数が有理数か無理数かを判定するのはなかなか困難である。たとえば、円周率πが無理数であることを証明するのはむずかしい。オイラーの定数γなどは、いまだに、有理数か無理数かがわかっていない。

［竹之内脩］

[参照項目] | オイラーの定数 | 指数関数 | 実数

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

無理数
むりすう
irrational number

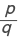整数 p と 0でない整数 q を用いて， と表すことができる数を有理数といい，有理数でない実数を無理数という。小数では，無理数は循環（→循環小数）しない無限小数として表される。√2＝1.41421356…，円周率π＝3.14159265…，自然対数の底 e＝2.7182818…などは無理数であることが知られている。実数は，有限小数または無限小数として表される数で，数直線上の点と一対一に対応するが，有理数から出発して，収束する有理数列の極限を付け加えることによって構成される。厳密な構成法としては，コーシー列（→コーシーの条件）を用いて完備化する方法，ユリウス・W.R.デデキントが導入した切断による方法などがある。有理数を係数とする代数方程式の解となる数を代数的数といい，そうでない実数を超越数と呼ぶ。超越数は無理数である。上の無理数の例のうち，√2は方程式 x²－2＝0 の解の一つであるから代数的数である。円周率π，自然対数の底 e は超越数であることが知られている。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

無理数 (むりすう)
irrational number

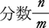（m，nは整数でm≠0）の形で表せない実数，すなわち，有理数以外の実数を無理数という。例えば，\(\sqrt{2}\)や\(\sqrt{3}\)は無理数である。自然数aが他の自然数のn乗で表せないときn\(\sqrt{a}\)は無理数であり，この形の無理数を不尽根数という。また，無理数の中には自然対数の底eや円周率πなどのように超越数と呼ばれるものもある。無理数は小数で表すと，循環しない無限小数で表されるが，逆に循環しない無限小数は無理数である。

　実数αは整数mと0≦β＜1であるような実数βの和として表される。このmをαの整数部分といい，［α］で表す。この記法による［　］をガウス記号という。β＝α－［α］をαの小数部分という。集合｛nα－［nα］｜n＝1，2，……｝を考えると，これはαが有理数のときには有限集合となるが，無理数のときには無限集合となり，これによっても有理数と無理数が区別される。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

無理数【むりすう】

有理数でない実数。分数n/m（n，mは整数かつm≠０）で表せない数。つまり小数で表したとき有限小数や循環小数にならない数。（式１），円周率π，自然対数の底eなど。→実数／無理式
→関連項目e｜循環小数

出典　株式会社平凡社

世界大百科事典（旧版）内の無理数の言及

【数】より

…7世紀にインドで負の数の導入がなされ，それがアラビアへ8世紀ころ伝わり，その後ヨーロッパへ伝わったのが12世紀ころといわれている。無理数についていえば，面積に関して開平，体積に関して開立，直角に関して三平方の定理はいずれもある程度古代中国でも古代ヨーロッパでも知られていたようであるが，近似値には着目しても，無理数概念の確立には至っていなかった。とくにヨーロッパでは，三平方の定理に関連して，ピタゴラスはという無理数の存在を知ったが，当時線分の長さは，それに含まれる点の数に比例するという信仰があり，が分数で表せないことの意味がわからなくて苦しんだという。…

※「無理数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」