関連語
精選版 日本国語大辞典 「絶対値」の意味・読み・例文・類語
ぜったい‐ち【絶対値】
ブリタニカ国際大百科事典 小項目事典 「絶対値」の意味・わかりやすい解説
絶対値
ぜったいち
absolute value; modulus
 である。 (2) 複素数 α=a+ib ( a ,b は実数) においては,その絶対値を
である。 (2) 複素数 α=a+ib ( a ,b は実数) においては,その絶対値を 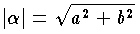 と定義する。
と定義する。 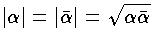 (
( 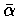 はαの共役複素数) である。αが実数のときは b=0 であるから
はαの共役複素数) である。αが実数のときは b=0 であるから 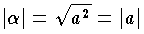 となり,実数の絶対値の定義に一致する。いま Z=a+ib をガウス平面上の点 P(a,b) で表わすと
となり,実数の絶対値の定義に一致する。いま Z=a+ib をガウス平面上の点 P(a,b) で表わすと 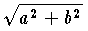 は原点Oから点Pまでの距離に等しい。 (3) ベクトルの長さをベクトルの絶対値ということもある。
は原点Oから点Pまでの距離に等しい。 (3) ベクトルの長さをベクトルの絶対値ということもある。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
日本大百科全書(ニッポニカ) 「絶対値」の意味・わかりやすい解説
絶対値
ぜったいち
実数aに対して、aまたはその符号を変えた-aのうち、負でないほうを、aの絶対値といい、|a|のように表す。つまり、|a|は、aが正のときはa自身、aが負のときは-a、aが0のときは0である。数直線上で考えるときは、aの絶対値は原点0と点aとの距離を表す。
二つの実数a、bの計算と絶対値の間には次の関係がある。まず、乗法・除法については二つの積・商の絶対値は、それぞれ絶対値の積・商に等しい。
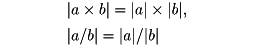
ただし、bは0でないとする。加法・減法については、二数の和・差の絶対値は絶対値の和以下、差以上である。
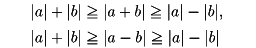
実数以外に対しても絶対値が定められる。複素数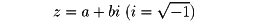
に対して、zの絶対値|z|を、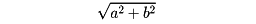
と定める。zの絶対値は、zを複素平面上に表すとき、原点と点zの距離を表す。
[三輪辰郎]
改訂新版 世界大百科事典 「絶対値」の意味・わかりやすい解説
絶対値 (ぜったいち)
absolute value
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「絶対値」の意味・わかりやすい解説
絶対値【ぜったいち】
出典 株式会社平凡社百科事典マイペディアについて 情報
冬に 4日間暖かい日が続くと 3日間寒い日が続き,また暖かい日が訪れるというように,7日の周期で寒暖が繰り返されることをいう。朝鮮半島や中国北東部の冬に典型的な気象現象で,日本でもみられる。冬のシベリ...


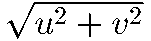 に等しい。
に等しい。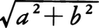 で定め,|α|で表す。αの絶対値は0または正の数であり,αが0のときに
で定め,|α|で表す。αの絶対値は0または正の数であり,αが0のときに